5.2.2 LR-Family: SLR(1) Table Generation

At any stage of the parse, we will have the following configuration:

        Stack                  Input
        s0x1s1...xmsm            aiai+1...$

where the s's are states, the x's are sequences of terminals or nonterminals, and the a's are input symbols. This is somewhat like a finite-state machine where the state on top (the right here) of the stack contains the "accumulation of information" about the parse until this point. We just have to look at the top of the stack and the symbol coming in to know what to do.

We can construct such a finite-state machine from the productions in the grammar where each state is a set of Items.

We create the table using the grammar for expressions above. The reader is asked in Exercise 2 to extend this to recognize a sequence of assignment statements.

States

The LR table is created by considering different "states" of a parse. Each state consists of a description of similar parse states. These similar parse states are denoted by marked productions called items.

An item is a production with a position marker, e.g.,

        E 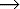 E · + T

which indicates the state of the parse where we have seen a string derivable from E and are looking for a string derivable from + T.

Items are grouped and each group becomes a state which represents a condition of the parse. We will state the algorithm and then show how it can be applied to the grammar of Example 3.

Algorithm

Constructing States via Item groups

(0) Create a new nonterminal S' and a new production S' S where S is the Start symbol

(1) IF S is the Start symbol, put S' · S into a Start State called State 0.

(2) Closure: IF A x · X is in the state, THEN add X · to the state for every product X · in the grammar.

(3) Look for an item of form A x · z where z is a single terminal or nonterminal and build a new state from A --> xz · ( Include in the new states all items with · z in the original state.)

(4) Continue until no new states can be created. (A state is new if it is not identical to an old state.)

Example 4 Constructing items and states for the expression grammar

Step 0 Create E' E

Step 1

State 0

E' · E

Step 2

E · E fits the model A x · X , with x, = , and X = E. E T and E E + T are productions whose left-hand sides are E; thus E · T and E · E + T are added to State 0.

State 0

E' · E

E · E + T

E · T

Reapplying Step 2 to E · T adds

T · T * F

T · F

and reapplying Step 2 To T · F adds

F · (E)

F · Id

State 0 is thus:

State 0

E" · E

E · E + T

E · T

T · T * F

F · (E)

F · Id

If the dot is interpreted as separating the part of the string that has been parsed from the part yet to be parsed, State 0 indicates the state where we "expect" to see an E (an expression). Expecting to see an E is the same as expecting to see an E + T (the sum of two things), a T (a term), or a T · F (the product of two things) since all of these are possibilities for an E (an expression).

Using Step 3, there are two items in State 0 with an E after the dot. E' · E fits the model A x · z with x and = , z = E. Thus, we build a new state, putting E' E · into it. Since E · E + T also has E after ·, we add E E · + T. Step 2 doesn't apply, and we are finished with State 1.

State 1

E' E ·

E E · + T

Interpreting the dot , ·, as above, the first item here indicates that the entire expression has been parsed. When we create the table, this item will be used to create the " Accept" entry. (In fact, looking at the table above, it can be seen that "Accept" is an entry for State 1.) Similarly, the item E E · + T indicates the state of a parse where an expression has been seen and we expect a " + T". The string might be "Id + Id" where the first Id has been read, for example, or Id * Id + Id * Id where the first Id * Id has been read.

Continuing, the following states are created.

State 2              State 3         State 4         State 5         State 6
E  T ·        T  F ·        F  (· E)   F  Id ·       E  E + · T
T  T · * F                     E  · E + T             T  · T * F
                                E  · T                 T  · F
                                T  · T * F                     F  · (E)
                                T  ·  F                        F  · Id
                                F  · (E)
                                F  · Id

State 7                  State 8       State 9           State 10        State 11
T     T  * · F F  ( E · )     E  E + T ·     T  T * F ·     F  (E) ·
F  · (E)       E  E · + T     T  T  · * F    
F  · Id

These are called LR(0) items because no lookahead was considered when creating them.

We could use these to build an LR(0) parsing table, but for this example, there will be multiply defined entries since the grammar is not LR(0) see (Exercise 10) These can also be considered SLR items and we will use them to build an SLR(1) table, using one symbol lookahead.

Algorithm

Construction of an SLR(1) Parsing Table

(1) IF A x · a is in state m for input symbol a, AND A x a · is in state n, THEN enter Sn at Table [m,a].

(2) IF A · is in state n, THEN enter Ri at Table [n,a] WHERE i is the production i : A and a is in FOLLOW (A).

(3) IF S' S · is in State n, THEN enter "Accept" at Table [n, $].

(4) IF A x · B is in State m, AND A x B · is in State n, THEN enter n at Table [m, B].

Example 5 Creating an SLR(1) table for the expression grammar

Following are some of the steps for creating the SLR(1) table shown in Example 4. One example is shown for each of the steps in the algorithm.

Step 1

E  E · + T is in State 1
E  E + · T is in State 6

so Table[1,+] =S6

Step 2

In State 3 we have T F ·

The terminals that can follow T in any sentential form are +, *, ), and $ (see Chapter 4)

So Table[3,+] = Table[3,*] = Table[3,)] = Table[3,$] = R4 where 4 is the number of production T F.

Step 3 E' is the Start symbol here and E' E · is in State 1, so Table[1,$] ="Accept"

Step 4

E · E + T is in State 0, while E E · + T is in State 1, so Table[0,E]=1