5.2.1 LR-Family: Parser Driver

The driver reads the input and consults the table. The table has four different kinds of entries called actions:

Shift:

Shift is indicated by the "S#" entries in the table where # is a new state. When we come to this entry in the table, we shift the current input symbol followed by the indicated new state onto the stack.

Reduce:

Reduce is indicated by "R#" where # is the number of a production. The top of the stack contains the right-hand side of a production, the handle. Reduce by the indicated production, consult the GOTO part of the table to see the next state, and push the left-hand side of the production onto the stack followed by the new state.

Accept:

Accept is indicated by the "Accept" entry in the table. When we come to this entry in the table, we accept the input string. Parsing is complete.

Error:

The blank entries in the table indicate a syntax error. No action is defined.

Using these actions, the driver algorithm is :

Algorithm
LR Parser Driver

Initialize Stack to state 0
Append $ to end of input
While Action <> Accept And Action <> Error Do

Let Stack = s₀x₁s₁...x_ms_m and remaining Input=a_ia_i+1...$

{S's are state numbers; x's are sequences of terminals and nonterminals}

Case Table [s_m,a_i] is

S#: Action : Shift

R#: Action : = Reduce

Accept : Action : = Accept

Blank : Action : = Error

EndWhile

Example 3 LR parsing

Consider the following grammar, a subset of the assignment statement grammar:

1. E --> E+T
2. E --> T
3. T --> T * F
4. T --> F
5. F --> (E)
6. F --> Id

and consider the table to be built by magic for the moment:



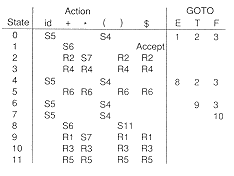
We will use grammar and table to parse the input string, a * ( b + c ), and&127; to understand the meaning of the entries in the table:

Step (1)

Parsing begins with state 0 on the stack and the input terminated by "$":

Stack                        Input                   Action
0                       a * (b + c) $           

Consulting the table, across from state 0 and under input Id, is the action S5 which means to Shift (push) the input onto the stack and go to state 5.

Step (2)

Stack                        Input                   Action
(1) 0                   a * (b + c) $           S5
(2) 0 id 5              * (b + c) $ 

The next step in the parse consults Table [5, *]. The entry across from state 5 and under input *, is the action R6 which means the right-hand side of production 6 is the handle to be reduced. We remove everything on the stack that includes the handle. Here, this is id 5. The stack now contains only 0. Since the left-hand side of production 6 will be pushed on the stack, consult the GOTO part of the table across from state 0 (the exposed top state) and under F (the left-hand side of the production). The entry there is 3. Thus, we push F 3 onto the stack.

Step (3)

(2) 0 id 5              * (b + c) $             R6
(3) 0 F 3               * (b + c) $

Now the top of the stack is state 3 and the current input is *. Consulting the entry at Table [3, * ], the action indicated is R4, reduced using production 4. Thus, the right-hand side of production 4 is the handle on the stack. The algorithm says to pop the stack up to and including the F. That exposes state 0. Across from 0 and under the right-hand side of production 4 (the T) is state 2. We shift the T onto the stack followed by state 2.

Continuing,

(3)     0  T 3                  * (b + c) $             R4
(4)     0  T 2                  * (b + c) $             S7
        0  T2  * 7                (b + c) $             S4
        0  T2  *  7 (4            (b + c) $             S5
        O  T2  *  7 (4id 5          +  c) $             R6
        0  T2  *  7 (4F3            +  c) $             R4
        0  T2  *  7 (4T2            +  c) $             R2
        0  T2  *  7 (4E8            +  c) $             S6
        O  T2  *  7 (4E8 + 6           c  $             S5
        O  T2  *  7 (4E8 + 6 id 5      )  $             R6
        O  T2  *  7  (4E8 + 6F 3       )  $             R4
        O  T2  *  7  (eE8 + 6T9        )  $             R1
        O  T2..*  7  (4E8)             )  $             S11
        O  T2  *  7  (4E8  11             $             R5
        O  T2  *  7F10                    $             R3
        O  T2                             $             R2
(19)    O  E1                             $             Accept

Step (19)

The parse is in state 1 looking at "$". The table indicates that this is the accept state. Parsing has thus completed successfully. By following the reduce actions in reverse, starting with R2, the last reduce action, and continuing until R6 the first reduce action, a parse tree can be created. Exercise 1 asks the reader to draw this parse tree.

---