|
| 4.0 Introduction |
4.2 LL(1) Parser Driver
Top-down parsing proceeds by expanding productions, beginning with the start symbol. The grammar must be LL(1)
In order to define LL(1), we need two preliminary definitions: FIRST and FOLLOW. FIRST is defined for a sentential form; FOLLOW is defined for a nonterminal.
FIRST(
), for any sentential form , is the set of terminals that occur left-most
on any string derivable from including 
if is derivable from .
For a nonterminal A in a sentential form, say 
A
where and are some string of terminals and nonterminals,
FOLLOW(A) = FIRST()
That is, FOLLOW(A) is the set of terminals that can appear to the right of A in a sentential form.
A grammar is LL(1) if and only if given any two productions A 
, A 
,
(a) FIRST ()
FIRST( ) = 
,
and
(b) If one of or derives ,
- ...
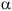
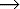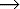
then FIRST(
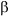)FOLLOW(A) = .Elimination of left-recursion and left-factoring aid in producing an LL(1)grammar. If the grammar is LL(1), we need only examine the next token to decide which production to use. The magic table contains a production at the entry for Table[Nonterminal, Input Token].
Top-down parsing uses a stack of symbols, initialized to the start symbol.
Algorithm
LL(1) Parser Driver
Push a $ on the stack. Initialize the stack to the start symbol. REPEAT WHILE stack is nonempty: CASE top of the stack is: terminal: IF input symbol matches terminal, THEN advance input and pop stack, ELSE error nonterminal: Use nonterminal and current input symbol to find correct production in table. Pop stack Push right-hand side of production from table onto stack, last symbol first. END REPEAT If input is finished, THEN accept, ELSE error
Send questions and comments to: Karen Lemone
