

By Carolina Ruiz, Samuel Ogden and Ahmedul Kabir
Due Dates:
Canvas Initial Submission: by Wednesday, Sept. 27th, 2017 at 11:00 pm
Canvas Tournament Submission: by Wednesday, Oct. 11th, 2017 at 12:00 NOON (no late submissions will be accepted)

PROJECT DESCRIPTION AND GOAL
This project consists of developing and implementing
a computer program that plays Gomoku.
Gomoku, also known as "five in a row",
is a board game similar to tic-tac-toe but on a larger board. The project will exemplify the minimax algorithm and alpha-beta pruning.
GAME DESCRIPTION
(For simplicity, the following game description will use "it" to refer to a player, as the player will be
a computer program you'll write.)
-
Gomoku is a two player game (one of them being your computer program).
The two players take turns putting markers ("stones") on a board.
- One of the players uses white stones and the other one uses black stones.
- Stones are put on the cells of a 15 X 15 board. Columns are marked with letters A ... O from left to right and rows are numbered 1 ... 15 from top to bottom
- A move can be specified by the column letter and row number pair (e.g., F 8)
- The player who
first gets 5 of its stones contiguously in a row (horizontally, vertically or diagonally) wins. If neither player wins before the board completely fills up, the game ends in a tie.
A possible state of the game is shown in the following figure
![[ Example 15 X 15 Board ]](Gomoku-board.png)
A possible board configuration for a Gomoku game in a 15 X 15 board
GAME RULES
A game will consist of a sequence of the following actions:
- A random selection method is used to determine which player will use the white
stones and which player will use the black stones.
In what follows, the player who gets to use the white stones
is called player1 and the player who gets to use
the black stones is called player2.
- Player1 gets to play first.
- After player1 has made its first move, player2 is
given the chance to change the color of the stone on the board
to black. This is done to limit the advantages of playing first.
For example, if player1 places its first white stone at E7 and
player2 decides that it wants that position, then
player2 can place its first black stone at E7.
This is the only time during the game that a player is allowed
to put a stone in an already occupied cell.
-
After that, players 1 and 2 take turns making moves.
A move should satisfy the following
constraints:
- Time Limit
There is a 10 second time limit for a player to make its move.
- Move preconditions
- The color is white if it is player1's turn and
black if it is player2's turn.
- The cell at the intersection of column and row
on the board is empty. (The only potential exception to this precondition
is during player2's first move as described above.)
- Move postconditions
- After the move, the cell at the intersection of column and
row
on the board will be occupied by a stone of the color representing the player who made the last move.
- It will be the other player's turn.
- The game ends when either of the following two cases happen:
-
one of the players gets five of its stones contiguously in
a row (vertically, horizontally, or diagonally). This player wins
the game, and the other loses the game.
- all the cells on the board are occupied and no player got 5 stones in a row. In this case,
the game ends in a tie .
The project assignment consists of the following:
- Your group must implement a program that plays Gomoku.
- Each group needs to pick a one-word name for its program.
- Your program must use the minimax algorithm with alpha-beta pruning.
- Use a utility function (i.e., static evaluation) of your choice.
- If your minimax with alpha-beta pruning cannot expand the whole search
tree in the time allowed, your program should use a game strategy:
- Use an evaluation function of your choice to be able to evaluate intermediate nodes and thus avoid expanding the whole minimax tree.
Remember that your evaluation function should coincide with (i.e., be equal to) your utility function on terminal board configurations.
- Also, implement heuristics to decide which nodes in the game tree to continue expanding and which nodes not to expand any further.
For sample evaluation functions and heuristic game strategies, study Sections 5.3.1, 5.4.1 and 5.4.2 of Russell and Norvig's textbook and investigate approaches described in other online sources.
The better your evaluation function and your heuristic game strategy, the
better your program will play, and the better your grade in the project.
- Your program must produce only valid moves.
- Your program must be able to read each of the opponent's moves, and should execute them. (The process is described in the following section.)
- Your program must follow the specification given in this project so that it can
interface with other groups' programs.
- If you want, you may implement a graphical interface for your program,
that displays the configuration of the board during the game.
Such an interface is NOT required.
(As described below, a referee program will be provided which will display the board during a game.)
There are many communication methods that are far more elegant and
efficient than this one, but the intent is that this method will result in the
least elaborated code, and that it allows you to implement your program in
your choice of programming languages. All the moves are communicated through a file accesible to both players.
- Each group needs to pick a one-word name for its program.
We'll refer to that name as groupname in what follows.
- Each group must submit the code of its program and an executable (or
script) named groupname.
- A referee program, described below, will be told what two groups are going to play.
The referee will decide at random which player goes first, check the validity of the moves, check for game ending conditions, and maintain the communication between the two groups' programs.
The referee program will be provided and posted to this webpage soon. You do NOT have to write the referee program.
In most parts of this document, we will
refer to the referee program as "the referee" or simply "Referee".
- The referee will maintain four text files: a file called move_file , two groupname.go files (one for each group) and an end_game file that will be created upon the completion of the game and which will contain the final outcome of the game (e.g., the winning player, if any).
Note: not all four of these files will exist at all times as they are used to control the flow of turns. Please see below for more details.
- The presence of a groupname.go file indicates that it is that player's turn. When groupname.go file appears in the directory, the groupname's program should first check to see if an end_game file exists. If this file exists, it means that the game is over and this file contains the result of the game as described below. If the end_game file doesn't exist then the groupname's program should read the opponent's move from move_file,
pick its own move, and overwrite move_file with its own move. When groupname.go is absent in the directory, the groupname's program should simply wait for it to appear.
- A move will have the following format: <groupname> <column> <row> (e.g., "myGroup B 4" but without the " " around the move)
- At the beginning of the game, each program should wait until the file groupname.go with its groupname appears in the directory.
The program then reads move_file . If this file is empty, then the program plays with white stones and hence makes the first move.
Otherwise, if a move already exists in move_file , then the program plays with black stones.
- Each program is allowed a maximum of 10 seconds to make its move. The timer starts as soon as the groupname.go file appears,
and a move is considered done 100 ms after a write to move_file is made.
(This is because the referee polls move_file every 50 ms to see if its timestamp has changed.
After it detects a change it then waits 100 ms to allow the team to finish writing out their move and then reads the move from the file. This allows the player program
time to write out in case the polling happened right as they opened the file.
The player programs' file write should NOT take any longer than 100 ms. The program needs to open the file for writing, write the move and close the file all in one concise operation to ensure the referee reads in what they mean.
- The two groups' programs now take turns making moves until the end_game fle is created.
The possible messages the referee can write on the end_game file are:
- END: <winning_groupname> WINS! <losing_groupname> LOSES! <reason>
where reason can be any of the following:
- Five in a row!
- Time out!
- Out-of-order move!
- Invalid move!
- END: Match TIED. Board full!
- To summarize, each group's program does the following
- Wait until groupname.go appears in the directory
- Read in the move from move_file and calculate its own next move using minimax with alpha-beta pruning
- Write its move to move_file (overwriting the content of that file)
- Repeat until the end_game file is created by the referee announcing that the game is over!
For illustration purposes, here is an example sequence of events that happens in a game between
two groups GroupX and GroupY.
- GroupX and GroupY programs start and wait for their respective "go" files.
- Referee starts and creates the file move_file. Referee then randomly selects a group as the first player. Let's assume that player is GroupX.
- Referee creates the file GroupX.go and starts timing.
- GroupX detects the presence of the GroupX.go file, reads move_file, finds out it is empty, and knows it is the first player.
- GroupX calculates its move (let's say D 3) and writes in move_file the line "GroupX D 3" (without the " ") within 10 seconds.
- The current content of move_file is
GroupX D 3
- Referee detects a change in move_file, waits 100 ms, reads the move, checks timing and validity of move, checks if the game has ended.
- Since the game hasn't ended yet, Referee deletes the GroupX.go file and creates GroupY.go.
- GroupY detects the presence of the GroupY.go file, reads move_file, finds out it is NOT empty, and knows it is the second player.
- GroupY reads GroupX's move, calculates its own move (let's say E 4) and writes in move_file the line "GroupY E 4" (without the " ") within 10 seconds. (As per the game's rules, GroupY could have chosen as its move D 3 if it wanted.)
- The current content of move_file is
GroupY E 4
- The process above is repeated until there is an invalid / late / out-of-order move, or if someone wins, or if the board is full.
In each of these cases, the referee program
creates the end_game file and writes a corresponding message to it as described above. The referee also creates both groupname.go files so that both players are prompted to look for the end_game file. Let's suppose GroupY wins.
Then the end_game file will contain:
END: GroupY WINS! GroupX LOSES! Five in a row!
- All programs stop running.
A referee program to conduct the game will be provided. The functions of the referee
have been detailed in the previous section.
Specifically, the referee program will be in charge of:
- Assigning which program goes first, as described above.
- Displaying a graphical depiction of the board configuration after each move.
- Giving turns to each of the playing programs. By creating
the file groupname.go, the referee program is giving
the turn to groupname.
- Timing each of the players. It starts measuring the time
for groupname's move just after creating groupname.go.
If a program exceeds its time limit, the referee program
will stop the game, announcing that the offending program
has lost. (Note that your program should not time its opponent.)
- Detecting invalid moves. If the referee program
finds an invalid move, it will stop the game, announcing
that the offending program has lost.
- Ending the game when all positions on the board are
occupied, announcing a tie.
- Ending the game when one of the programs makes 5 stones
in a row, announcing the winner and loser.
This referee program can be found in the github repository at https://github.com/samogden/WPI.CS4341.git.
If you find any issues or bugs with this referee program, or any deviations from the specifications provided on this webpage, PLEASE report them on the Canvas discussion board immediately. In such event, we will try to fix any bugs, update the version of the referee program in GitHub and notify the class.
By Wednesday, Sep 27 at 11 pm,
one (and only one) member of your group must submit the following
files using Canvas:
- The names of the members of your group
- Instructions on compiling and running your program
- The utility function that your program uses
- The evaluation function that your program uses
- The heuristics and/or strategies that you employed to decide how to expand (pieces of) the minimax tree without
exceeding your time limit
- Results:
- describe which tests you ran to try out your program.
Did your program play against human players?
Did your program play against itself?
Did your program play against other programs?
How did your program do during those games?
- describe the strengths and the weaknesses of
your program.
- A discussion of why the evaluation function and the heuristic(s) you picked are good choices.
Finding a good static evaluation function and a good heuristic
depends heavily on the experience you have with the game.
We recommend you start playing the game and getting the flavor
of what a good Gomoku strategy is. Also, research the strategies
that other people have used for this and other games.
Lots of information can be found in the references listed in
your syllabus, the web, and magazine articles.
- Code.
- The source code for your program
- Ancillary files, if any, that your program requires (e.g., such as a script to run a language interpreter).
Please note: Although you are welcome to look at code and systems available online to guide the
design of your program, you MUST submit your own original code.
- A tournament will be held where the students' programs will compete against each other!
- Each group will be allowed to keep working on and improve their programs submitted for Project 2.
Before the tournament, all groups will submit the updated tournament version of their code via Canvas. The
deadline for making the submissions is Wednesday, Oct 11 2017 by 12:00 noon.
Note however that the majority of your project grade will come from your initial project 2 submission. See Grading Criteria below.
- The final rounds of the tournament will be held during class on Oct 12 2017.
- Groups whose program perform well in the tournament will receive bonus points.
- More details about the structure and the logistics of the tournament will be provided in due time.
MORE details about the tournament have now come...
- Tournament Rules:
- You must submit via Canvas by the re-submission deadline either a new, improved player
or a note asking us to use your original player in the tournament.
- Your player must not consume computing resources during your opponent's
turn. In this spirit, when it is your opponent's turn, your player
should simply check for the signal from the referee that it is your turn to move.
- Both players will be executed on the same machine, and must not spawn
processes on any other machine.
- The new player you submit on Oct. 11th will play against your original player from Sept. 27th.
- If your new player wins, then your group will earn 5 points (see full list of extra points below in the Grading Criteria).
- The winner of this match will represent your team in the tournament.
- Tournament Structure:
- Each CS4341 section will play its own separate tournament.
- The tournament structure will mimic that of soccer's World Cup,
but the precise structure will be determined when we know how many players will participate.
However, every participating player is guaranteed at least 2 games.
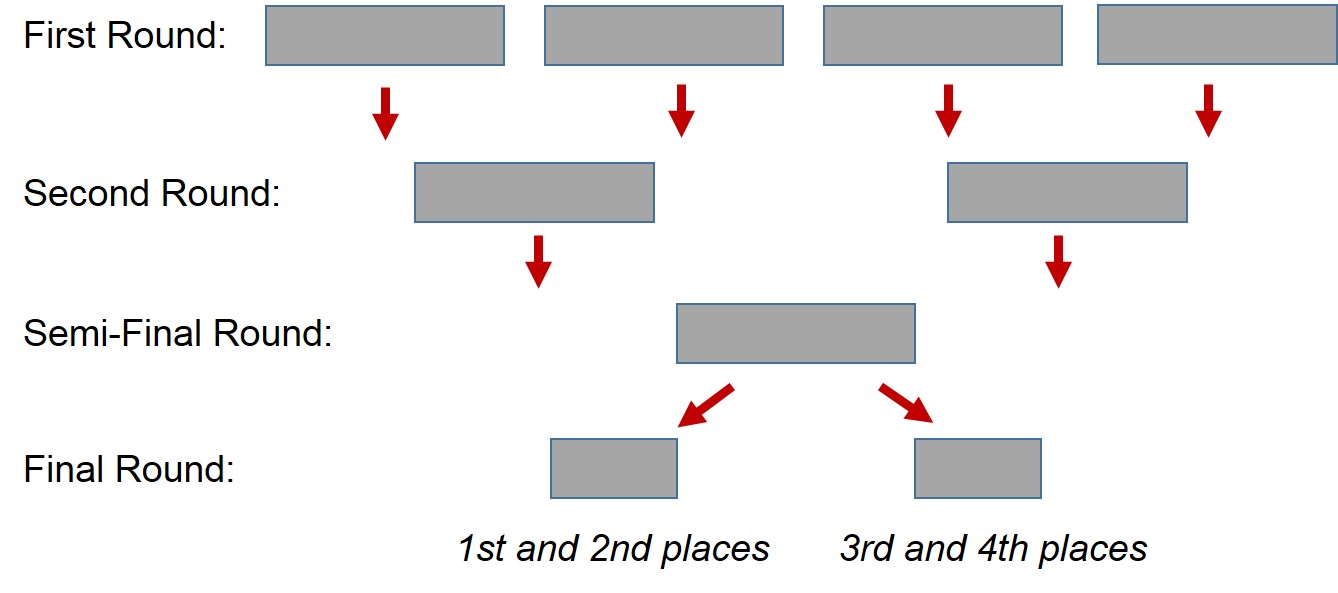
- First Round:
Each player will be randomly assigned to one of 4 groups of either 3 or 4 players.
Each player will play against every other player in its group.
- Second Round:
The best 2 players in each group from the first round will move on to this round.
Each of these 8 players will be assigned to one of 2 groups of 4.
Each player will play against every other player in its group.
- Semi-Final Round:
The best 2 players in each group from the second round will move to this round.
Each of these 4 players will play against every other player in this group.
- Final Round:
The bottom 2 players from the semi-final round will play each other for the third place, and
the top 2 players from the semi-final round will play each other for the first place.
- "In the end, there can be only one." :-)
- Tournament Date and Time:
- First, Second, and Semi-Final Rounds will be held on Wednesday afternoon,
October 11th promptly after we receive your submissions.
Results from these rounds will be announced in clas on Thursday, Oct. 12th
(but not before then).
- Unless one of the finalist teams object,
the Final Round games will be played in class on Thursday, Oct. 12th.
GRADING CRITERIA:



![[ Example 15 X 15 Board ]](Gomoku-board.png)
