cs2223 Class 10 - a Summation

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes] [Class 10]

cs2223, D97/98 Class 10, a Summation

Note: This page contains an attached Excel spreadsheet. A zip version is also atached for those whose browsers do not reliably download spreadsheet files.

Start with

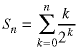
S(n) = sum(k=0->n; k/(2^k))

Notice how we added a term to make the lower limit zero, instead of one. We can do that because this term is zero (since k is zero). The next term in the sequence is:

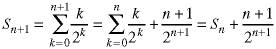
S(n+1) = sum(k=0 -> n+1; k/(2^k)) = sum(k=0 -> n; k/(2^k)) + (n+1)/(2^(n+1))) = S(n) + (n+1)/(2^(n+1)))

This gives us a recurrence relation:

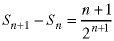
S(n+1) - S(n) = (n+1)/(2^(n+1))

In standard form, the recurrence relation is:

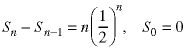
S(n) = S(n-1) = n * (1/2)^n, S(0) = 0

This is one of the forms which can be calculated exactly using the techniques shown in the recurrence relation notes. The solution is:

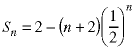
S(n) = 2 - (n+2) * (1/2)^n

This solution can be proven inductively. The attached spreadsheet shows it is numerically correct for the first few terms.