For the first two cases, the line or polygon is simply added to the appropriate node of the tree. If the line or polygon is coincident, it can be handled by storing multiple polygons in the node of the BSP tree. If the polygon spans the hyperplane, the polygon splitting algorithm must find the intersection point of the polygon and plane. This can be done with ray plane intersection approach for convex polygons.
Finally, the BSP tree algorithm can perform either recursively or iteratively. The recursive BSP tree is very simple to understand because it simply performs a partition based on the current hyperplane and then recurses the the front and back leaf nodes. The following sample code illustrates this:
bsp_tree(poly* current_poly)
{
while(still_polygons)
{
partition_polygons(current_poly);
}
bsp_tree(current_poly->left);
bsp_tree(current_poly->right);
}
However, for performance reasons, recursion is not always attractive.
In most situtations, BSP tree calculations are done prior to
interactive rendering of a scene. However, if dynamic objects are
inserted into the tree, BSP tree calculations may need to be done in
real time. According to [4], recursion can be modelled by a
stack. As you want to traverse down the BSP tree, you push the
pointer of the node onto the stack.
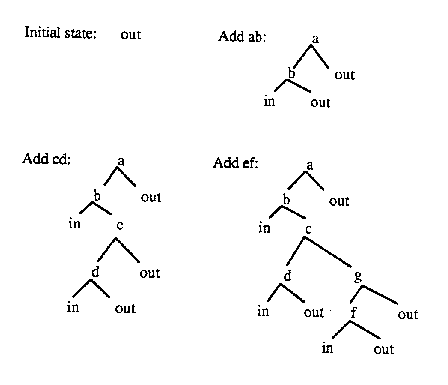
In order to really understand how a BSP tree works, it helps to see a graphical demonstration of tree creation. The following set of images show how in a 2 dimensional example lines would be added to the bsp tree.
First, create a root node and partition plane.
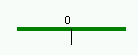 |
Obviously the root does not have any children. |
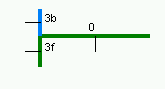 |
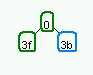 |
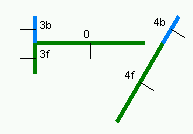 |
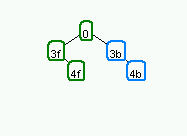 |
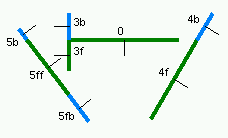 |
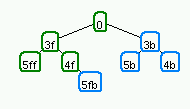 |
Using a BSP for rendering a scene
Improving rendering performance is one of the reasons BSP trees are used. BSP trees essentially peform extensive precalculation for a back to front painters algorithm or a front to back scanline algorithm. The tree can be traversed in linear time from an arbitrary viewpoint.
Since a painters algorithm works by drawing polygons farthest from the eye first, the following code recurses to the bottom of the tree and draws the polygons. As the recursion unwinds, polygons closer to the eye are drawn over far polygons. Because the BSP tree allready splits polygons into trivial pieces, the hardest part of the painters algorithm is allready solved.
code for back to front tree traversal.
traverse_tree(bsp_tree* tree,point eye)
{
location = tree->find_location(eye);
if(tree->empty())
return;
if(location > 0) // if eye infront of location
{
traverse_tree(tree->back,eye);
display(tree->polygon_list);
traverse_tree(tree->front,eye);
}
else if(location < 0) // eye behind location
{
traverse_tree(tree->front,eye);
display(tree->polygon_list);
travers_tree(tree->back,eye);
}
else // eye coincidental with partition hyperplane
{
traverse_tree(tree->front,eye);
traverse_tree(tree->back,eye);
}
}
According to [4],
BSP trees can also be used to render a scene with a front to back
traversal of the tree using a scanline fill algorithm. A write mask
can be used to prevent a pixel from being written to more than once.
In a scene with many light sources, the painters algorithm would
evaluate the same pixel more than once.
In order to traverse the tree from front to back, simply change the order of the recursion in the above code.
Shadow generation using BSP trees
While BSP trees are useful for fast hidden surface removal in static scenes, they can also be used to compute shadows with one or more fixed light source. Conventional methods for shadow generation form a shadow polygon from two vectors emmanating from the point light source and the vertices on an object's edges [1]. The shadow volume is clipped against the view volume (the screen, a floor, a wall, etc) to create a finite volume. Any polygon inside a shadow polygon is in shadow. All visible points on a scene polygon are tested against the relative number of shadow polygons between it and the eyepoint to determine if the point is in shadow [1]
The above approach takes two passes: one to construct shadow volumes and another to test points against shadow polygons. The scene also must be transformed by the light source's perspective transformation. Most shadow volume approaches require clipping against polygons instead of planes as in the BSP approach.
The Shadow Volume BSP Tree algorithm proposed by Chin and Feiner does not require clipping against a view volume or any kind of tranformation of the scene. Basically, the SVBSP approach creates a merged shadow volume during the process of inserting polygons into the BSP tree. The SVBSP can be precalculated as long as the scene and light source(s) are static.
The SVBSP tree algorithm has a shadow plane at each internal node.
The shadow plane is defined by the a point light source and an edge of
the polygon. The direction of the plane's normal determines if an
object is in or outside of shadow.
There are two main steps to the SVBSP algorithm:
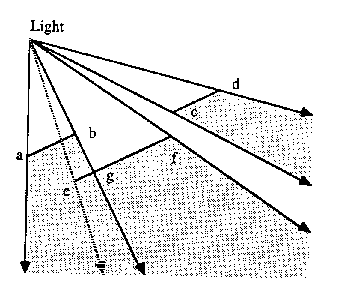
- Determining shadows: the polygon is filtered down the SVBSP tree to determine if it is lit or shadowed. if the polygon is both in shadow and light, it is split into two polygons. Note that if a polygon is in front of the eye and its shadow volume is allready defined by a polygon closer to the light source, the farther polygon can be discarded. This can be seen in the example when line ef are added into the SVBSP tree.
- Enlarging the SVBSP tree: Once a polygon has been filtered through the SVBSP tree, its shadow volume is computed and inserted into the tree. In the case of segment eg in the example below, the shadow volume is allready inside another shadow volume and does not need to be included.
Multiple Light Sources
SVBSP trees can be easily extended to multiple light sources.
Basically, construct a SVBSP tree with the first light source. Store
all polygon fragments at the appropriate node of the BSP tree which
defines the scene. Once all polygons have been partitioned, throw
away the current SVBSP tree. Next, create a SVBSP tree from the next
light source. Filter the polygon fragments into this new tree.
Repeat until there are no more light sources and there is a final
SVBSP ready for shadow generation.
Chin and Feiner warn that multiple light sources could result in a very large tree with many split polygons. They recommend that light sources be processed in order that will lead to the least fragmentation. One method is to process the light sources in increasing order with the number of polygons facing them. Alternatively, process static light sources first and dynamic sources last.
all source code is from Near Real-Time shadow Generation Using BSP Trees by Chin and Feiner. The shadowGenerator creates shadow volumes by applying the recursive function determineShadow to all scene polygons. determineShadow filters the polygons down the SVBSP tree splitting them when necessary and adding shadow volumes of lit fragments to the SVBSP tree.proecedure shadowGenerator(PLS,BSPtree) ;Initialize the SVBSP tree to an OUT cell SVBSPtree := OUT ;Process all polygons facing light source PLS in ;front-to-back order by BSP tree traversal in 0(n) for each scene polygon p, in front-to-back order relative to PLS if p is facing PLS ;Determine areas of p that are shadowed. ;BSPnode is p's node in BSPtree SVBSPtree := determineShadow(p,SVBSPtree, PLS,BSPnode) else ;p is not facing PLS or PLS is in p's plane mark p as shadowed endif endfor endproc
;determineShadow filter p down SVBSPtree to ; dtermine shadowed fragments and reattaches shadowed ;fragments to BSPnode procedure determineShadow(p,SVBSPnode,PLS,BSPnode) returns SVBSPnode if(SVBSPnode is an IN cell) attach p to BSPnode as a shadowed fragment else if(SVBSPnode is an OUT cell) attach p to BSPnode as a lit fragment ; create shadow volume for p and ; append it to the SVBSP tree shadowPlanes := planes that form the shadow volume of p with PLS SVBSPnode := buildSVBSPtree(SVBSPnode,shadowPlanes) else ; split p by SVBSPnode.plane, creating ; negPart and posPart splitPolygon(p, SVBSPnode.plane, negPart,posPart) if(negPart is not null) SVBSPnode.negNode := determineShadow(negPart, SVBSPnode.negNode,PLS,BSPnode) if(posPart is not null) SVBSPnode.posNode := determineShadow(posPart, SVBSPnode.posNode, PLS, BSPnode) endif endproc
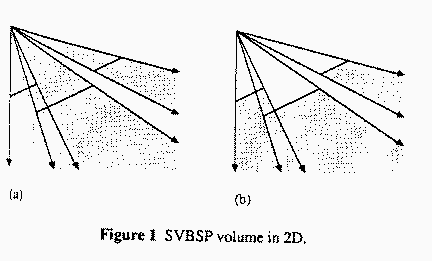
Dynamic changes in a scene using BSP trees
As shown in the above sections, BSP trees are excellent algorithms for hidden surface removal in rendering and shadow generation. However, since many applications want to have dynamic interaction with the world that is created, some method needs to be applied to handling dynamic objects.
One method proposed by Fuchs et. al. was to specify a bounding polygon around the area that of the scene that would be changing. Since the standard BSP algorithm does not interact with the insides of polygons, the programmer can manipulate the environment inside the polygon. One example wold be to place a long rectangular polygon over a road in a static world scene. The render could be specially modified to tree the bounding polygon as a special case and would know how to update the contents inside the polygon. Another approach would be to have a seperate hidden surface removal algorithm for dynamic objects. For instance, in a doom type world, the level could be in a BSP tree while all missles and bullets could be rendered using a z-buffer.
in [2], Y. Chrysanthou et al. describe three criteria necessary for to support dynamic changes in 3D scenes:
- Ability to change the camera view
- ability to add an object into the scene
- ability to delete an object from the scene
fortunately, there is a solution for deleting nodes from a BSP tree. There are four cases for deleting
- on a leaf node. Simply delete this polygon because it does not have any children who partition other polygons nor is it partitioned itself.
- on a node with other coincidental faces (on the same plane). This is also easy since the partition hyperplane is defined by the other polygons stored in that node.
- a node with exatly one non-empty child. This is easy because the hyperplane of this node split the subspace into a empty and non-empty region. Simply, the child of the deleted node becomes the child of the parent of the deleted node.
- a node with two non empty children. This is the most challenging problem because a polygon could have been split by the hyperplane of this node. Fortunately, the polygons can be reconstructed by filtering the smaller sub tree into the larger sub tree. The larger sub tree takes the place of the deleted node. The FilterIntoTree performs this processes.
performance issues
Polygons who are near the leaf-nodes of the BSP tree can be deleted in
constant time. Consequently, objects that are transient should be
inserted into the BSP tree last. The FilterIntoTree function may also
be fairly slow and costly when the smaller trees it is merging may be
transient. Y. Chrysanthou et al. mention that an alternative startegy
could be employed that would adopt criteria to determine when the
filtering operation should be carried out. One approach is to just
mark a node as deleted but not actually remove it from the tree.
ANother approach is to only filter when the sub tree is less than a
maximum size.
function TidyTree(tree)
{
if Empty(tree) then return EMPTY_TREE endif;
if tree.root is not market as "deleted" then
tree.front = TidyTree(tree.front);
tree.back = TidyTree(tree.back);
return(tree);
else
if any child of the tree is empty then
return(TidyTree(other child of tree))
else return(FilterIntoTree(polygons of smaller sub-tree,
TidyTree(largest subtree)))
endif
enif
}
modified tidytree algorithm that only runs if the sub-tree size gets too large:
if tree.root is not market as "deleted" or the smaller sub-tree is too large then tree.root = TidyTree(tree.front); tree.back = TidyTree(tree.back); return(tree); else ...
Excellent BSP java demo
BSP Frequently Asked Questions
Inside Quake: Visible Surface Determination
Binary Space Partitioning page
3D Engines List
[1] Chin, N., and Feiner, S., Near Real-Time Shadow Generation Using BSP Trees, Computer Graphics (SIGGRAPH '89 Proceedings), 23(3), 99-106, July 1989.
[2] Chrysanthou, Y., and Slater, M., Computing Dynamic Changes to BSP trees, Computer Graphics Forum (EUROGRAPHICS '92 Proceedings), 11(3), 321-332, sep 1992.
[3] Fuchs, Henry., et. al. Near Real-Time Shaded Display of Rigid Objects, Computer Graphics, 17(3), 65-69.
![[Return to CS563 '97 talks list]](/images/back.gif)