Building a heap
-
Inserting elements one at a time - must maintain the heap properties
-
cost: q(n lgn)
-
Heapifying an array containing the values to be stored in the heap
-
approach starting from the deepest level, sift the root of a subtree down to its position
-
Cost: q(n)
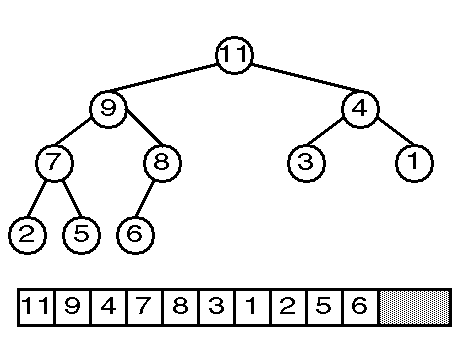
Example. Build a heap from:
2, 3, 1, 10, 9, 7, 8, 4, 6, 5
C++ class for a heap
class heap {
private:
Element* Heap;
int max_size;
int curr_size;
int is_leaf(int);
int parent(int);
int left_child(int);
int right_child(int);
void sift_down(int );
void build_heap();
public:
heap(int);
heap(Element*, int, int);
~heap();
int heap_size();
void insert(Element);
Element remove_max();
};
int heap::is_leaf(int n){
return (curr_size/2 <= n) &&
(n < curr_size);
}
int heap::parent(int n){
if ((0 < n) && (n < curr_size))
return (n - 1)/2;
else
return OUT_OF_RANGE;
}
int heap::left_child(int n){
if (2*n+1 < curr_size)
return 2*n+1;
else
return OUT_OF_RANGE;
}
int heap::right_child(int n){
if (2*n+2 < curr_size)
return 2*n+2;
else
return OUT_OF_RANGE;
}
void heap::sift_down(int n){
while (!is_leaf(n)){
Element temp; int i, left, right;
left = left_child(n);
if ((right = right_child(n)) !=
OUT_OF_RANGE)
if (Heap[left]>Heap[right]
i = left;
else
i = right;
else
i = left;
if (Heap[n] > Heap[i])
return;
else{
temp = Heap[n];
Heap[n] = Heap[i];
Heap[i] = temp;
n = i;
}
}}
void heap::build_heap(){
for (int i = curr_size/2-1 ; i >= 0 ; i--)
sift_down(i);
}
heap::heap(int size){
Heap = new Element[size];
max_size = size;
curr_size = 0;
}
heap::heap(Element* array,
int m_size, int c_size){
Heap = array;
max_size = m_size;
curr_size = c_size;
build_heap();
}
heap::~heap(){
delete []Heap;
}
int heap::heap_size(){
return curr_size;
}
void heap::insert(Element v){
Element temp;
Heap[curr_size] = v;
for (int i = curr_size ; (i > 0) &&
(Heap[i] > Heap[parent(i)]) ;
i = parent(i)){
temp = Heap[i];
Heap[i] = Heap[parent(i)];
Heap[parent(i)] = temp;
}
curr_size++;
return;
}
Element heap::remove_max(){
Element temp;
if (curr_size > 0){
curr_size--;
temp = Heap[0];
Heap[0] = Heap[curr_size];
Heap[curr_size] = temp;
sift_down(0);
return(Heap[curr_size]);
}
else
return OUT_OF_RANGE;
}