Binary Trees

Objectives:

to define the binary tree ADT
to present particular types of binary trees
to describe different implementations of binary trees and analyze those implementations
to present some applications of binary trees

Definitions and Properties

Definition. A binary tree is a finite set of nodes connected by edges such that:

the set is either empty or consists of a node called the root and two binary trees, called the left and right subtrees, which are disjoint from each other and the root;
there is an edge from the root to the roots of its subtrees.

Terminology:

children of a node - the roots of its subtrees (a node is called parent of its children)
path - a sequence of nodes n1,n2,...,nk such that ni is the parent of ni+1 for all 0<i<k
length of a path - the number of edges along it
a node A is an ancestor of another node B if there is a path from A to B (B is a descendant of A)
depth of a node - the length of the path from the root to that node

height of a tree - one more than the length of its deepest node
level - the set of nodes of a given depth
leaf node - has both its children empty
internal node - has at least one non-empty child

Special binary trees

full binary tree: each node is either a leaf, or an internal node and has exactly two non-empty children

complete binary tree: all the levels are completely filled, excepting possibly the deepest one, which is filled from the left to the right

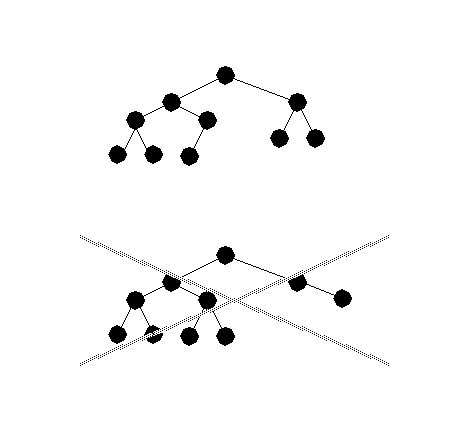
Characterization of binary trees

Theorem. The number of leaves in a non-empty full binary tree is one more than the number of internal nodes.

Proof. By mathematical induction on the number of internal nodes.

Base:

Induction hypothesis: assume that a full binary tree containing n-1 internal nodes has n leaves
Induction step:

Theorem. The number of empty subtrees in a non-empty binary tree is one more than the number of nodes in the tree.

Proof.

every node of a binary tree has two children, for a total of 2n children for a binary tree of n nodes.
every node, except for the root node has one parent, for a total of n-1 parents (n-1 nonempty children)
results that the remaining n+1 children (2n-(n-1)) must be empty

Theorem. Any binary tree with n leaves has an average height of at least lgn.

Proof.

let T be a binary tree with n leaves and denote by H(T) the sum of depths of the leaves
we need to show that for a binary tree with n leaves

the root of T can have 0,1 or 2 children

let h(n) be the smalles value for H(T) when T is a binary tree with n leaves (define h(0)=0)

since i=0 and i=n cannotyield the minimum 0<i<n
prove by mathematical induction that

Binary tree traversals

Traversal: processing all the nodes in a systematic manner

Preorder traversal: visit the node first, then traverse its left subtree in preorder, then its right subtree in preorder

Postorder traversal: traverse the left subtree in postorder, then the right subtree in postorder, and finally visit the node itself

Inorder traversal: traverse the left subtree in inorder, then visit the node, and finally traverse the right subtree in inorder

preorder: 1,2,4,6,7,8,3,5
postorder: 6,8,7,4,2,5,3,1
inorder: 6,4,7,8,2,1,3,5

The binary tree ADT

Type: a set of binary trees

Operations:

insert a node
remove a node
find a node

Binary tree implementations

Pointer-based implementation

class BinNode{

public:

Element value;

BinNode* left;

BinNode* right;

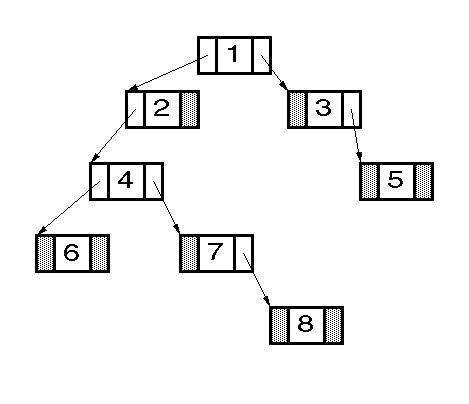
BinNode(){left = right = NULL;}

BinNode(Element e,

BinNode* l=NULL,

BinNode* r=NULL){

value = e; left = l; right = r;

}

~BinNode() {};

};

space requirement: n(2p+d), but can be reduced by eliminating pointers from leaf nodes (is this really true?)
Array-based implementation of complete binary trees
number the nodes level by level from the left to the right:

place the elements stored in the node in an array, at the index corresponding to the numbering

Calculating the indicex of relatives of a node:

parent(r)=(r-1)/2, if 0<r<n
left(r)=2r+1 if 2r+1<n
right(r)=2r+2 if 2r+2<n
left-sib(r)=r-1 if r -even, 0<r<n
right-sib(r)=r+1 if r -odd, r+1<n

Binary search trees

Definition. A binary search tree (BST) is a binary tree in which all nodes of the left subtree of a node store values less than the value stored in that node, and all nodes of the right subtree of a node store values greater than the values stored in that node.

inserting a value into a BST

deleting a node from a BST
deleting the minimal value

deleting an arbitrary node