RT. Run-Time Storage Management
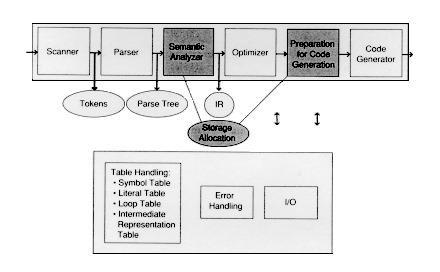
The previous sections of these modules presume that assembly language code is to be generated by our compiler. When this is done, we need not worry about allocating space for program quantities. The assembler and other system software take care of this. Production-quality compilers (usually) do not put out assembly language code. Instead, they emit object code directly. This section does not discuss object code formats for particular machines. Instead, we discuss how the compiler facilitates the storage of information that is to take place at run-time. All of these actions could be considered as part of either the semantic analysis phase or as preparation for code generation.
Values are assigned to variables at execution time, but it is the compiler, at compile time, which performs the necessary bookkeeping so that this happens smoothly.
If we consider a program as a sequence of "unit" calls (with the main program being the first unit), then we can see immediately some of the issues. Suppose a variable, declared to be of type integer, is assigned an integer-sized space in the machine. What happens if this unit is a procedure called recursively? Clearly, there must be more than one such space allocated for such a variable.
In this section, we will proceed from simple languages (simple storage-wise!) like FORTRAN, which do not allow recursion, to languages that allow recursion, and data structures like pointers whose storage requirement change during execution.
Decisions made at compile time include where to put information and how to get it. These are the same decisions made about symbol tables, but here the information is different. For symbol tables, we are concerned about information that is known at compile time, in particular the symbol's class. Here, we are concerned about information not entirely known at compile time, such as a particular symbol's value or how many instances there will be of a variable due to recursive calls.
Storage must be allocated for user-defined data structures, variable, and constants. The compiler also facilitates procedure linkage; that is, the return address for a procedure call must be stored somewhere.
This can be though of as binding a value to a storage location and the binding can be thought of as a mapping:
Source Language 
Target Machine
Thus, although some of the later optimization phase is independent of the machine, the run-time storage algorithms are somewhat machine dependent.
Many of the compile-time decisions for run-time storage involve procedure calls. For each procedure or function, including the main program, the compiler constructs a program unit to be used at execution time. A program unit is composed of a code segment, which is the code to be executed, and an activation record, which is the information necessary to execute the code segment.
A code segment is fixed since it consists of (machine code) instructions, while the activation record information is changeable since it references the variables which are to receive values.
The information in an activation record varies according to the language being compiled. An activation record can be of a fixed or variable size.
A typical activation record contains space to record values for local data and parameters or references to such space. It also contains the return location in the code so that execution can resume correctly when the procedure finishes.
The term offset is used to describe the relative position of information in an activation record, that is, its position relative to the beginning of the activation record.
Different languages have different needs at run-time. For example, the standard version of FORTRAN permits all decisions to be made at compile-time. (It doesn't require this to be done.)
We say that FORTRAN-like languages have static storage allocation. This means that at compile-time all decisions are made about where information will reside at run-time.
Because FORTRAN typifies the issues for static storage allocation, it will be used as the example here. For FORTRAN and other languages which allow static storage allocation, the amount of storage required to hold each variable is fixed at translation time.
Such languages have no nested procedures or recursion and thus only one instance of each name (the same identifier may be used in different context, however).
In FORTRAN each procedure or function, as well as the main program and a few other program structures not discussed here, may be compiled separately and associated with an activation record that can be entirely allocated by the compiler.
Example 1 shows the skeleton of a FORTRAN program and its storage allocation.
EXAMPLE 1 Static storage example
Consider the following outline of a FORTRAN program, where statements beginning with C represent comments.
C Main Program ... Read (*,X) ... C Function ... FUNCTION ... ... C Subroutine ... SUBOUTINE ... ...
For each program unit such as the main program, a function or a subroutine (procedure), there is a code segment and an activation record. Figure 1 is a picture of what the run-time system might look like for the program skeleton of Example 1:
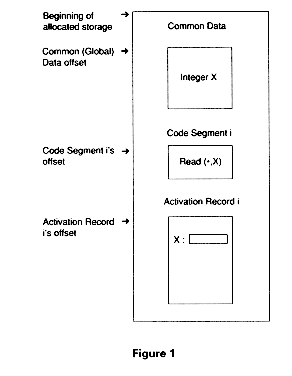
Figure 2 shows X's offset within the activation record:
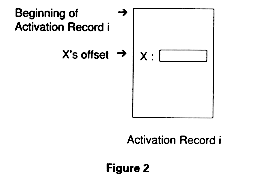
Notice that everything except the beginning of the allocated storage is known at compile-time: the position (offset) of the activation record within the data area and even X's position (offset) within the activation record for its unit. The only decision to be made at run-time (and often made by the system linker) is where to put the entire data structure.
In static storage allocation, variables are also said to be static because their offset in the run-time system structure can be completely determined at compile time.
For languages that support recursion, it is necessary to be able to generate different data spaces since the data for each recrusive call are kept in the activation record.
Such activation records are typically kept on a stack.
When there is more than one recursive call which has not yet terminated, there will be more than one activation record, perhaps for the same code segment.
An extra piece of information must thus be stored in the activation record -- the address of the previous activation record. This pointer is called a dynamic link and points to the activation record of the calling procedure.
Languages such as Algol, Pascal, Modula, C and Ada all allow recursion and require at least the flexibility of a stack-based discipline for storage.
Example 2 shows a program and its stack of activation records when the program is executing at the point marked by the asterisks. The program is not in any particular language, but is pseudocode.
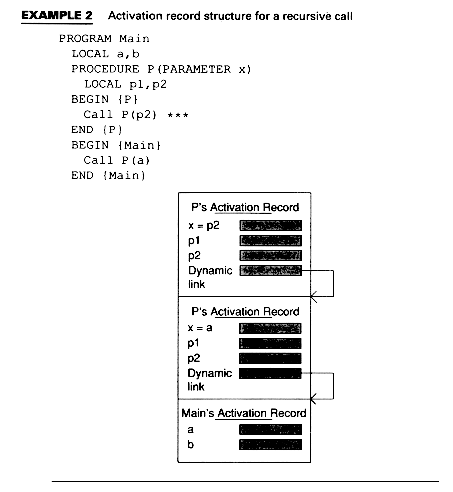
In Example 2, main's activation record contains space to store the values for the variables a and b. The activation record stacked on top of the activation record for main represents the activation record for the (first) call to P. P's parameter x has actual value a, and there is space for its value, as well as space for the local variables p1 and p2. The address of the previous activation record is stored in dynamic link.
On the other hand, the amount of storage required for each variable is know at translation time, so, like FORTRAN, the size of the activation record and a variable's offset is known at translation (compile) time. Since recursive calls require that more than one activation record for the same code segment be kept, it is not possible, as in FORTRAN, to know the offset of the activation record itself at compile-time. Variables in these languages are termed semistatic.
Block-structured languages allow units to be nested. Most commonly, it is subprograms (procedures) that are nested, but languages such as Algol and C allow a new unit to be created, and nested, merely by enclosing it with BEGIN-END, { }, or similar constructs.
The unit within which a variable is "known" and has a value is called its scope. For many languages a variable's scope includes the unit where it is defined and any contained units, but not units that contain the unit where the variable is defined.
During execution, block-structured languages cause a new complication since a value may be assigned or accessed for a variable declared in an "outer" unit. This is a problem because the activation record for the unit currently executing is not necessarily the activation record where the value is to be stored or found.
A new piece of information must be added to the activation record to facilitate this access. Pointers called static links point to the activation records of units where variables, used in the current procedure, are defined. Uplevel addressing refers to the reference in one unit of a variable defined in an outer unit. A sequence of static links is called a static chain.
Example 3 makes two changes to the program of Example 2. The variables a and b are now global to the program, and procedure P references variable a. An additional field, the static link, is shown in P's activation record.
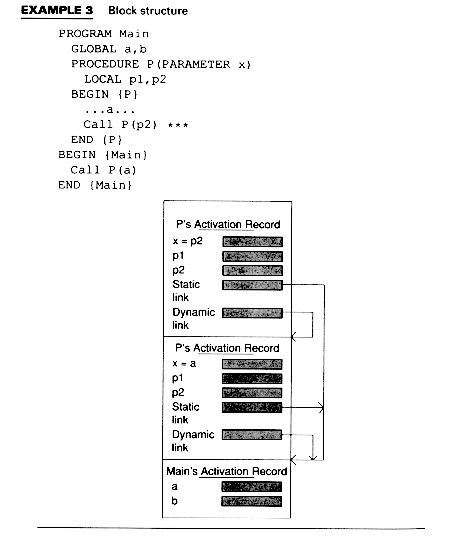
In Example 3, the static link points from the activation records for P to that for Main since P is nested within Main.
Once again though, the actual size of the activation record is known at compile-time.
There are language constructs where neither the size of the activation record nor the position of the information within the activation record is known until the unit begins execution.
One such construct is the dynamic array construct. Here, a unit can declare an array to have dimensions that are not fixed until run-time. Example 4 shows the program from Examples 2 and 3, with such a dynamic array declaration and its activation record structure.
In Example 4, the dimensions for P3 are known when procedure P is activated (called).
Clearly, if the values for array P3 are to kept in an activation record for P3, the size of the record cannot be fixed at translation time. If a is given a value within P, as well as within Main, it is possible that the activation record for P will be a different size for each invocation.
What can be created at compile-time is space in the activation record to store the size and bounds of the array. A place containing a pointer to the beginning of the array can also be created (this is necessary if there is more than one such dynamic structure). At execution time, the record can be fully expanded to the appropriate size to contain all the values or the values can be kept somewhere else, say on a heap (described below).
Variables, like the dynamic arrays just described, are called semidynamic variables. Space for them is allocated by reserving storage in the activation record for a descriptor of the semidynamic variable. This descriptor might be a pointer to the storage area as well as the upper and lower bounds of each dimension.
At run-time the storage required for semidynamic variables is allocated. The dimension entries are entered in the descriptor, the actual size of semidynamic variable is evaluated and the activation record is expanded to include space for the variable or a call is made to the operating system for space and the descriptor pointer is set to point to the area just allocated.
There are languages that contain constructs whose values vary in size, not just as a unit is invoked, as in the previous section, but during the unit's execution. C (and other language) pointers, flexible arrays (whose bounds change during execution), strings in languages such as Snobol, and lists in Lisp are a few examples. These all require on demand storage allcoation, and such variables are called dynamic variables.
Example 5 shows the problems encountered with such constructs.
EXAMPLE 5 Dynamic variables
PROGRAM Main
GLOBAL a,b
DYNAMIC p4
PROCEDURE P (PARAMETER x)
LOCAL p1,p2
BEGIN {P}
NEW (p4)
Call P(p2) ***
END {P}
BEGIN {Main}
Call P(a)
END {Main}
In Example 5, notice that p4 is declared in Main, but not used until procedure p. Suppose that the program is executing at the point where the asterisks are shown, using the stack of activation record structure as in the previous examples. Where should space for p4's value be allocated?
P's activation record is on top of the stack. If space for p4 is allocated in P, then when P finishes, this value will go away (incorrectly). Allocation space for p4 in main is possible since the static link points to it, but it would require reshaping P's activation record, a messy solution since lots of other values (e.g., the dynamic links) would need to be adjusted.
The solution here is not to use a stack, but rather a data structure called a heap.
Heap
A heap is a block of storage within which pieces are allocated and freed in some relatively unstructured way.
Heap storage management is needed when a language allows the creation, destruction or extension of a data structure at arbitrary program points. It isimplemented by calls to the operating system to create or destory a certain amount of storage.
We will discuuss more about heaps for Lisp-like programming languages.
Languages such as Ada, which allow concurrent execution of program units, pose additional storage allocation problems in that each concurrently executing unit (tasks in Ada) requires a stack-like storage.
One approach is to use a heap. Still another solution is to use a data structure called a cactus stack.
Lisp is a programming language whose primary data struture is a list. Druing execution, lists can grow and shrink in size and thus are implemented using a heap data structure.
Although we refer explicitly to Lisp here, we could equally well be discussing Snobol, a string-oriented language, or any other language that requires data to be created and destroyed during program execution.
In Lisp-like languages, a new element may be added to an existing list structure at any point, requiring storage to be allocated. A heap pointer, say, Hp, is set to point to the next free element on the heap. As storage is allocated, this pointer is continually updated. Calls to operating system routines manage this allotment.
Certainly, if storage is continually allocated and not recovered, the system may soon find itself out of space. There are two ways of recovering space:explicitly and garbage collection, a general technique used in operation system. We will discuss these two as they relate to Lisp.
Explicit Return of Stroage
Consider the list 
in Figure 4, where each element contains two fields: the information
field and a field containing a pointer to the next element of the list. The element
, itself, points to (contains the address of) the first element in the list.
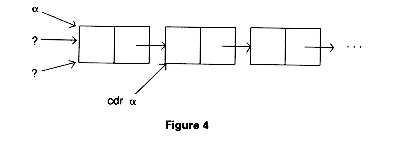
In LISP, an operator called (for historical reasons) cdr, given a pointer to one element in a list, returns a pointer to the next element on the list.
The question is whether or not cdr should cause the pointer to be returned to the
heap.
If is the only pointer and cdr doesn't return it to the heap, then it becomes
"garbage" (a technical term whose meaning should be clear!).
However, if cdr does return it and other pointers (shown as "?" in the picture
above) do exist, then they become dangling references; they no longer point to
because it no longer exists.
Unfortunately, it is difficult to know, although some creative (and time consuming!) bookkeeping could keep track. The alternative is to allow garbage to be created and periodically to "clean up"- a method called garbage collection.
Garbage Collection
When the garbage collection method is used, garbage is allowed to be created. Thus, there is no dangling reference problem.
When the heap becomes exhausted (empty), a garbage collection mechanism is invoked to identify and recover the garbage. The following describes a garbage collection algorithm. It presumes that each element in the system has an extra bit called a "garbage collection bit" initially set to "on" for all elements.
Algorithm
Garbage Collection
Step 1. Mark "active" elements, that is, follow all active pointers, turning "off" of the garbage collection bits for these active elements.
Step 2. Collect garbage elements, that is, perform a simple sequential scan to find elements with garbage bit on and return them to the heap.
The previous sections have discussed storage allocation "in the large", that is , the general activation record mechanisms necessary to facilitate assignment of data to variables.
Here, we disucss one issue "in the small", that of computing the offset for an element in an array. Other data structures such as records can be dealt with similarly (see
Computation of Array Offsets
Array references can be simple, such as
A[I]
or complex, such as
A[I - 2, C[U]]
In either case the variables can be used in an equation that can be set up (but not evaluated) at compile-time.
We will do this first for an array whose first element is assumed to be at A[1,1,1,...,1].
That is, given an array declaration
A: ARRAY [d1, d2, ... dk] OF some type
what is the address of
A[i1, i2, ... ik]?
It is easiest to think of this for the one- or two-dimensional case. For two dimensions, what is the offset for
A[i1,i2], given a declaration A: ARRAY[d1, d2] OF some type
By offset, we mean the distance from the base (beginning) of the array which we will call base (A).
To reach A[i1, i2] from base (A), one must traverse all the elements in rows 1 through i1 - 1 plus all the columns up to i2 in row i1. There are d2 elements in each of the i1 rows; thus, A[i1, i2]'s offset is:
(i1 - 1) * d2 + i2
The absolute address is
base (A) + (i1 - 1) * d2 + i2
For k-dimensions that address is:
base (A) + ((((i1 - 1) * d2 + (i2 - 1)) * d3 + (i3 - 1))
* d4 + ...) * dk + ik
or
base (A) + (i1 - 1) * d2d3...dk + (i2 - 1) * d3...dk + ...
+ (ik-1 - 1) * dk + ik
The second way is better for the optimization phase because the sum of indices is multiplied by constants, and these constants can be computed at compile time via constant computation and constant propagation.
In the next section, we discuss an implementation method using attribute grammars. This was touched upon in Module 6.
Computation of Array Offsets Using Attribute Grammars
Consider the following grammar for array references:
Name
We want to be able to attach attributes and semantic functions to these.
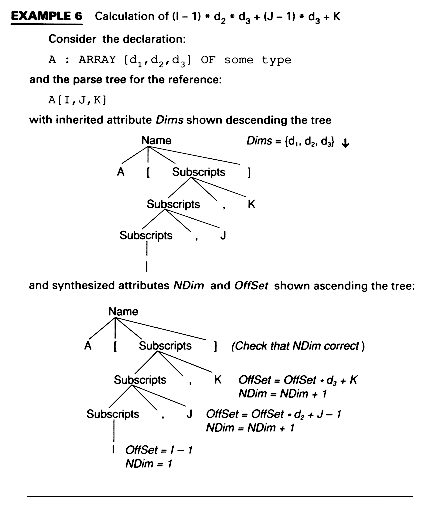
Example 6 shows a three-dimensional example and attributes Dims, NDim and Offset. Dims is an inherited attribute. It consults the symbol table at the node for the array name (A here) and fetches the values d1, d2, and d3 which are stored there. These are handed down the tree and used in the computation of Offset, which is a synthesized attribute. Attribute NDim is a counter that counts the number of dimensions, presumably for error checking.
