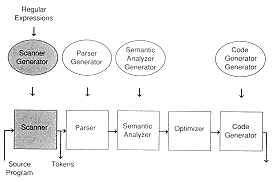
A scanner generator, also called a lexical analyzer generator, follows the form shown in Module 1:
In Figure 1, the scanner is shown in two parts - the table or program stub which is generated and the driver which is written, not generated.
The metalanguage for a scanner generator is a set of regular expressions describing the tokens in the language. A program stub or finite state table is generated from the regular expressions. At compile-time, the driver reads input characters from the source program, consults the table based upon the input and the current state, and moves to a new state based upon the entry, perhaps prforming an action such as entering an identifier into a name table.
We will illustrate these concepts with a sample language consisting of assignment statements whose right-hand sides are arithmetic expressions.
These regular expressions are input to the generator to produce state tables either in table form or as a case statement program stub.
These regular expressions are input to the generator to produce state tables either in table form or as a case statement program stub.
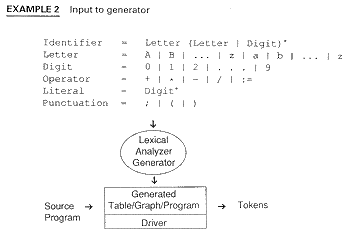
In Section Lex.2 and in Section Lex.3, we discuss the two programs, the driver program and the lexical analyzer generator.
In this section, we will presume the table has been created by magic. Rows in the table represent states, columns are input characters, and the entries in the table are states.
The lexical analyzer (the driver) considers the input source program as a long sequence of characters with two pointers: a current and a lookahead pointer:
When lexical analysis begins to find the next token, current and lookahead both point to the same character: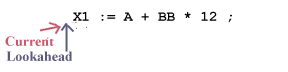 
In the algorithm, four actions are performed on these pointers:
WHILE there is more input
InputChar := GetChar
State := Table[0, InputChar]
WHILE State != Blank
InputChar := GetChar
State := Table[State, InputChar]
ENDWHILE
Retract
Accept
Return token = (Class, Value)
ENDWHILE
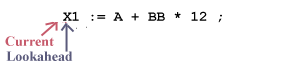
Before Retract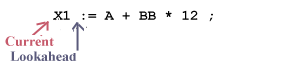 
After Retract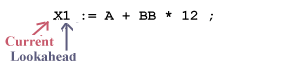 
After Accept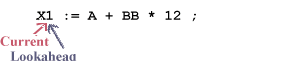 
The driver program scans the input program and comsults the entry at Table[State, InputChar] for the new state. The entry at Table[State, InputChar] consists of a new state and perhaps an action to be performed before moving to the new state:
In the algorithm retract is necessary when a token is found because the algorithm will have scanned one character too far.
The magically created table
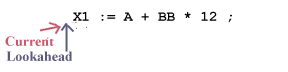
The entry there is state 1. The input looks like:
Since state entry is not blank, the algorithm enters the inner WHILE loop, and GetChar returns a new InputChar, the "1":
The driver continues and computes a new state, the entry at Table[1, digit,] which is also a "1". Thus on encountering a digit, the lexical analyzer stays in state 1. Returning to the condition in the inner WHILE, the algorithm computes that the state is still not blank; this GetChar returns the next character, either a space or, if all spaces have been removed, (See Exercise 2 ) the ";".
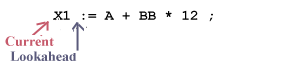
There is no entry at Table[1, space] or Table[1,:], so the condition in the inner WHILE fails and the algorithm executes the statements outside the inner WHILE, first performing a retract operation:
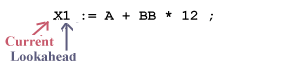
Then, the accept operation is performed, moving the current pointer ahead to the lookahead pointer:
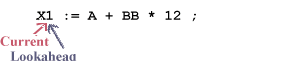
The token returned is that associated with state 1, probably a token with class equal to Id, and a value equal to the characters in the identifier or an index into a name table where the identifier is installed (See Exercise 3 )
The lexical analyzer driver now continues with the outer WHILE loop until input is exhausted.
Example Lex.3 shows a piece of a state table and the execution of the algorithm on an input string. Rows represent states, columns are input characters, and the entries in the table are states.
Section Lex.2 asks the reader to assume that the table is built by magic. The truth is that translating regular expressions to a state table or case statement is more tedium than magic. In this section, we will outline the steps and leave the algorithm to the reader (see Exercises 7 to 9 ).
Lexical Analyzer Generator Step 0: Recognizing a Regular Expression
A regular expression is either:
denoting the language consisting of the empty string (Sometimes 
is used to denote the empty string and the associated regular expression.) 
b (often the is omitted"). with a, with a a, with a a a, etc. and denoted a*.a* = {} U a U a a U a a a U ...
To convert a regular expression to a finite automaton requires the recognition of , |, * and as well as the individual characters in the sets. Recognition of is not really possible, so the resulting automaton will have to be converted to one which has no
- transitions.
There are six steps (a) - (f):
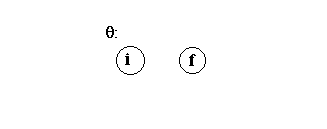
The diagram above shows that the regular expression is recognized by a nondeterministic finite automaton that has no way to get to a final state.
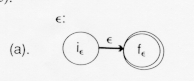
The diagram above shows that the regular expression is recognized by the nondeterministic finite automaton which goes from its initial state to its final state by reading no input. Such a move is called an - transition
In table form this would be denoted:
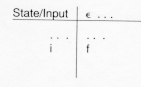
The reader may be wondering about an input of and how it would be recognized by the driver. In fact, it will not be. This is just a first step in table creation, and we will allow the creation of a nondeterministic finite automation (NFA). Section Lex.3.2 outlines how to turn this NFA into a deterministic finite automation (DFA)
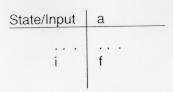
The diagram above shows that the language {a} denoted by the regular expression a is recognized by the finite automatation that goes from its initial to final state by reading an a. In table from this would be:
In the diagram above, we presume that the languages denoted by the regular expressions R
and R
, respectively, are recognized by the finite automata denoted by M and M.
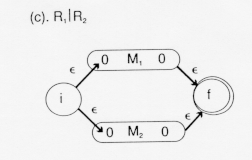
Adding -transitions to the beginning and end creates a finite automation which will recognize either the language represented by R
or the language represented by R, i.e., the union of these two languages, LR U LR.
We could eliminate the new final state and the -transitions to it by letting the final states of M and M remain final states.
In table form, this is:
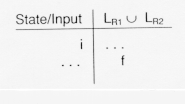
Here, the table entry for f is shown in a different row because the process of recognizing strings in either LR or LR may lead to other intermediate states.
Our example, which recognizes
Letters = A | B | C | . . . | a | b | . . . |z
and Literal = 0 | 1 | 2 | . . . | 9
will use this step.
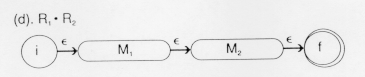
In the diagram above, M is the machine that accepts LR and M is the language that accepts LR. Thus, after this combined automation has recognized a legal string in LR, it will start looking for legal strings LR. This is exactly the set of strings denoted by R R. The related table is:
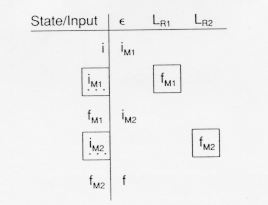
Here the table leads from an initial state, i, to the final state of M upon recognition of strings in LR, then from the final state in M, fM to the initial state in M on an -transition, that is, without reading any input, and then from the initial state in M, iM to the final state in M, fM upon recognizing the strings in LR. The is often omitted. It is understood that two regular expressions appearing next to one another represents the concatenation. We will use this step for the example, when we define an identifier as a string of letters and digits (conatenated). Another example will recognize a literal as the concatenation of one or more digits, that is,
Identifier = Letter (Letter | Digit) *
means
Identifier = Letter (letter | Digit) *
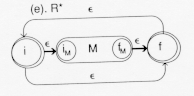
Here, M is a finite automation recognizing some LR. A new initial state is added leading to both M and to a new final state. The - transition recognizes the empty string, (if R did not contain already). The transition to M causes the language LR to be recognized. The transition from all final states of R to its initial state will allow the recognition of LR
, i = 1, 2,... The table is:
We will use this step as well as the preceding two, for the regular expressions
Identifier = Letter (Letter | Digit)*
and
Literal = Digit* = Digit Digit*
Using these diagrams as guidelines, we can "build" a nondeterministic finite automation from any regular expression (See Exercise 6
As we saw in
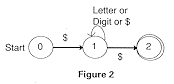
In Figure 2, one can go from state 1 to either state 1 or state 2 upon reading a "$".
These two possibilities, -transitions and multiple transitions on the same input, represent nondeterminism.
To convert from an NFA to a DFA, we eliminate these two possibilities by grouping states in the NFA. A state in the DFA will consist of a group (set) of states from the NFA.
The new start state is the same as the old start state.
With the new start state we group all the states we can get to upon reading the same input in the NFA; this process is continued with all the states of the NFA that are in any set of states in the DFA.
Any state in the DFA that contains a final state of the NFA is a final state.
For the NFA above, the new start state is 0', the prime to distinguish it from the old start state. State 1' = {1} since the only state accessible from state 0 in the NFA is state 1:
The situation is different for transitions from 1'={1}. Upon reading a letter or a digit, the transition is back to state 1. We can add that transition to the DFA:
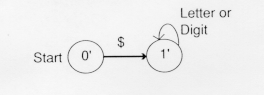
But there are two transitions upon reading "$" in the NFA, a move to state 1 and a move to state 2. We group these states into a new state called 2'={1, 2} in the DFA.
The DFA now is:
The state 2'={1,2} contains the old final state 2, so it is a final state.
If we are in state 2', so it is a final state. If we are in state2' = {1, 2} and the input is a letter or a digit, there is a transition back to 1' (because there is a transition from 1 to 1 in the NFA). Finally, there is a transition from 2' to 2' in the DFA upon reading a $ ( because there is a transition from 1 to 1 upon reading a $ in the NFA and 2'={1, 2}). The final DFA is:
This step of the lexical analyzer generator, conversion of a regular expression to a DFA, has shown the automata in the state-transition form. This could equally well have been shown in table form (See Exercise 7).
The step for removing -transitions is similar; all the states accessible via an -transition are grouped (See Exercise 6). This step can frequently result in DFA's with many states, some of which are performing the same function and can be combined. This is a necessary step in generating a lexical analyzer since there may be hundreds of states in the table for the tokens in a programming language.
A purist would not consider the above automation a true DFA since a true DFA will have a transition somewhere upon reading any character in the alphabet. Thus, state 0' should have an arrow (leading to an "error" state) upon reading a letter or a digit.
Minimizing a DFA consists of merging states which perform the same action. They can be found by repeated partitoning. We will show this for an NFA in table form. Final states 2 and 4 are shown in boldface:
The first step is to partition the table into final and non-final states:
The partioning continues by partitioning out states that lead to the same partition for the same input. Here, states 1, 3, and 5 lead to the last partitioned state upon reading a "$", while state 0 does not, so we put state 0 into a new partition:
All states in the second partition go to the same partition upon reading a letter or digit, and they all go to the third partition upon reading a "$". Thus, we are done, and relabeling the state table yields:
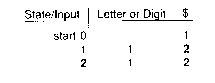
This concludes the minimization step (see Exercise 8 )and the procedure for conversion of a regular expression to a minimal finite automation, that is, we have described a lexical analyzer generator.
The only errors appropriately handled by a lexical analyzer are those which misuse a sequence of characters. Errors such as using a reserved word as an identifier are syntax errors to be found by the parser.
One way to handle errors is to define error tokens. For example, if the language does not contain a ".", a regular expression can be defined using one and the associated action would be to report an error.
Anticipating such user errors has met with limited success.
The reader may think it is much harder to write a lexical analyzer generator than it is just to write a lexical analyzer and then make changes to it to produce a different lexical analyzer. After all, most programming languages have similar tokens. This thought has been voiced by many compiler experts. In fact, many compiler tools allow the user to write lexical analyzer and call it from the generated parser or to make changes to a lexical analyzer provided by the tool.
Nevertheless, the process is informative, and there may be applications for which the user may wish to be able to generate various lexical analyzers.
The next section shows an example of a lexical analyzer generator, LEX (Lesk and Schmidt, 1975), a tool which comes with UNIX.
This section describes LEX, a lexical analyzer generator, written by Lesk and Schmidt at Bell Labs in 1975 for the UNIX operating system. It now exists for many operating systems, and versions can be obtained for almost any system including microcomputers. The discussion here is for illustration and should not be considered sufficient to use LEX.
LEX produces a scanner which is a C program (there are versions which produce other languages) that can be compiled and linked with other compiler modules. Other LEX-like tools exist which generate lexical analyzers in Pascal, Ada, C++, etc.
LEX accepts regular expressions and allows actions, code to executed, to be associated with each regular expression. At scan time, when an input string matches one of the defined regular expressions, the action code is executed.
The LEX metalanguage input consists of three parts: (1) definitions which give names to sequences of characters, (2) translation rules which define tokens and allow association of a number representing the class, and (3) user-written procedures in C which are associated with a regular expression. Each of these three sections is separated by a double percent sign, "%%". The input has the following form:
Definitions (Gives names to sequences of characters)
%%
Rules (Defines tokens. Class may be returned as a #)
%%
User-Written Procedures (In C)
The Definition section consists of a sequence of Names, each followed by an Expression to be given that name.
The Rules consist of a sequence of regular expressions, each followed by an (optional) action which returns a number for that regular expression and performs other actions if desired, such as installing the characters in the token into a name table.
The User-Written Procedures are the code for the C functions invokes as actions in the rules. Thus, the form for each section is: Name1 Expression1 C function1
Name1 Expression1
...
%%
RegExp1 {Action1}
RegExp2 {Action2}
...
%%
C function2
...
A section may be empty, but the "%%" is still needed.
Like UNIX itself, the metalanguage is case-sensitive, that is, "A" and "a" are read as different characters.
Example 4 shows a LEX description for our language consisting of assignment statements. There are other ways of expressing the tokens described here.
The C code scanner generated by LEX can be altered before it is compiled. The generated scanner is actually written to be "parser-driven"; when it is integrated into a compiler front end, it is invoked by the parser.
Figure 3 shows how the tool operates. These steps may vary from system to system:
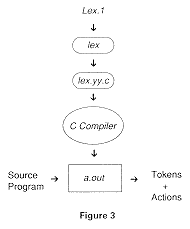
The LEX metalanguage description is input in a file called lex.1. LEX produces a file called lex.yy.c. The generated lexical analyzer is in UNIX's executable file called a.out.
Within the generated lex.yy.c is a C function called yylex() which performs GetChar and other actions discussed in Section Lex.2
The resulting scanner matches the longest input sequence. If two regular expressions match a particular input, then the first one defined is used. There are many more details of LEX's functionality to be described, and the reader is invited to look at a user's manual for any available LEX to which you may have access.
This has been an introduction to lexical analyzer generators and the process of converting from a regular expression to a minimal DFA, which is the lexical analyzer. This conversion is so complicated that many computer scientists advocate writing a lexical analyzer and then making changes to it for new applications. This works well for applications where the tokens are quite similar.
The process of generating a lexical analyzer has been likened to the compiler process itself:
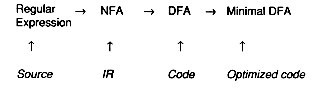
There are several lexical analyzer generators on the market, making it unlikely that anyone except a compiler tool designer or student in a sadistic instructor's class would ever have to write one.