8.6.5 Depth-First Order and Depth-First Spanning Trees
Intuitively, we begin at the start node and attempt to get as far away as possible. As
we proceed, we can make a (yet another!) tree from the arcs of the flow graph. This
is called a depth-first spanning tree, DFST.
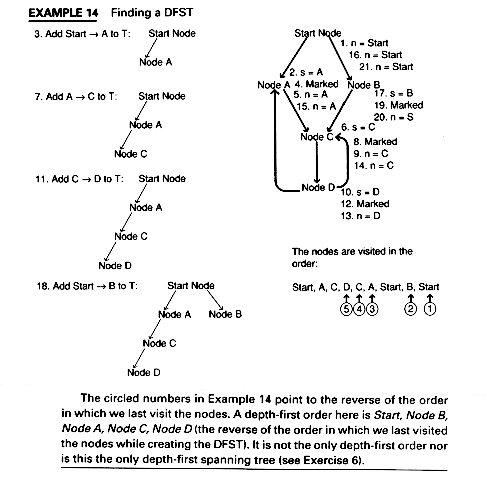
A depth-first order is defined to be the reverse of the order in which we last visit
the nodes of the control graph when we create the DFST. The following algorithm
creates a depth-first spanning tree.
T := empty
n := Start node
REPEAT
IF n has an unmarked successor s THEN
BEGIN
Add n 
s to T
Mark s
n := s
END
ELSE
n := parent of n in T
UNTIL n = start node and n has no unmarked successors
Exercise 4 asks the readers to compute dominators by visiting the nodes in a
somewhat random order and then to compute dominators by visiting the nodes in a
depth-first order. For some graphs, the algorithm terminates faster when the nodes
are visited in a depth-first order than when they are visited in the order Start, Node A,
Node B, Node C, Node D.
