8.6.3 Dominators
A node d dominates a node n, written d DOM n, if every path from the start node to n goes through d. This means that a node dominates itself. Example 11 shows dominators for the graph of Example 10.
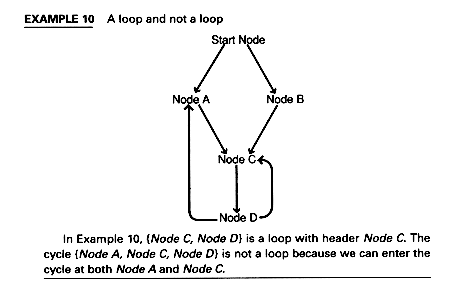
Here, the start node dominates all nodes; Node A and Node B do not dominate anything except themselves, Node C dominates Node D and itself, and Node D does not dominate anything except itself.
Note that for a node to dominate a node n, it must be n or dominate every predecessor of n. We use this fact to create an algorithm to find the dominators in a control flow graph. We use the notation Dom(n) for the set of dominators of a node n
Algorithm
Finding Dominators
DOM (Start) := {Start}
FOR node <> Start DO
DOM (node) = {All nodes}
ENDFOR
WHILE changes to any DOM(node) occur DO
FOR each node <> start DO
DOM(node) = {node} 
( 
Dom(p) )
p 
Pred(node)
ENDFOR
ENDWHILE
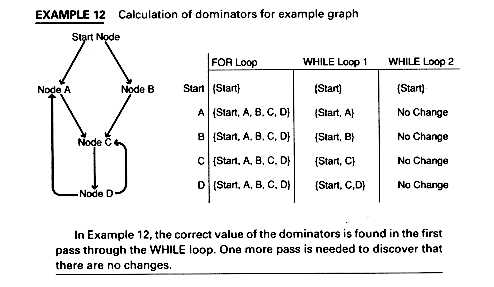
This algorithm for computing dominators does not indicate in what order to visit the node, just that all nodes are visited. In a later section, we will discuss an order for which this algorithm converges rapidly. Example 12 shows dominators being calculated for the graph of Example 11.
