8.5.7 Benefits of DAGs
When a DAG is created, common subexpressions are detected. Also,
creating a DAG makes it easy to see variables and expressions
which are used or defined within a block.
DAGs also produce good code at code generation time. In Module
11, we will see a code generation algorithm which produces good
(but not optimal!) code from a DAG.
Example 6 shows a bubble sort procedure and a set of quadruples
to which it might be translated. Quadruples are an intermediate
representation consisting of a single operation, up to two operands
and a result. They are easier for humans to read than an abstract
syntax tree. The quadruples shown here are in "assignment statement" form.
EXAMPLE 6 IR for a bubble sort procedure
FOR I := 1 TO n - 1 DO
FOR J := 1 TO I DO
IF A[J] > A[J+1] THEN
BEGIN
Temp := A[J]
A[J] := A[ J + 1 ]
A[ J + 1 ] := Temp
END
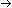 I := 1
GOTO ITest
ILoop: J := 1
GOTO JTest
JLoop: T1 := 4 * J
T2 := A [T1] ; A[J]
T3 := J + 1
T4 := 4 * T3
T5 := A[T4] ; A[ J + 1 ]
IF T2 <= T5 GOTO JPlus
T6 := 4 * J
Temp := A[T6] ; Temp := A[J]
T7 := J + 1
T8 := 4 * T7
T9 := A[T8] ; A { J + 1 ]
T10 := 4 * J
A[T10] := T9 ; A[J] := A[ J + 1 ]
T11 := J + 1
T12 := 4 * T11
A[T12] := Temp ; A [ J + 1 ] := Temp
JPlus: J := J + 1
JTest: IF J < = I GOTO JLoop
IPlus: I := I + 1
ITest: IF I <= n - 1 GOTO ILoop
I := 1
GOTO ITest
ILoop: J := 1
GOTO JTest
JLoop: T1 := 4 * J
T2 := A [T1] ; A[J]
T3 := J + 1
T4 := 4 * T3
T5 := A[T4] ; A[ J + 1 ]
IF T2 <= T5 GOTO JPlus
T6 := 4 * J
Temp := A[T6] ; Temp := A[J]
T7 := J + 1
T8 := 4 * T7
T9 := A[T8] ; A { J + 1 ]
T10 := 4 * J
A[T10] := T9 ; A[J] := A[ J + 1 ]
T11 := J + 1
T12 := 4 * T11
A[T12] := Temp ; A [ J + 1 ] := Temp
JPlus: J := J + 1
JTest: IF J < = I GOTO JLoop
IPlus: I := I + 1
ITest: IF I <= n - 1 GOTO ILoop
The intermediate code shown in Example 6 is rather high-level. For machines which have no indexing modes, the references to A[...] will have to be computed by the compiler. Also, the IF statements really involve several quadruples (see Module 6). The multiplication by "4" could, alternatively, be done at code generation time. We do it here because it will give us more opportunities for optimization of our example.
Using "( )" to mean "contents of " and "addr" to mean "address of", the low-level quadruples for "Temp := List[i]" might be:
T1 := addr(List)
T2 := T1 + I
temp := (T2)
Similarly, if the array reference is on the left-hand side of an assignment statement as in "List[i] := temp", low-level quadruples would be:
T1 := addr (List)
T2 := T1 + I
(T2) := Temp
Even if a machine has an indexing addressing mode, translating array references into their low-level format may allow optimizations (for example, if the subscript reference were a common subexpression).
Nevertheless, there will be numerous opportunities to improve the code sequence in Example 6.
Example 7 shows the basic blocks and the control flow graph for the procedure in Example 6.
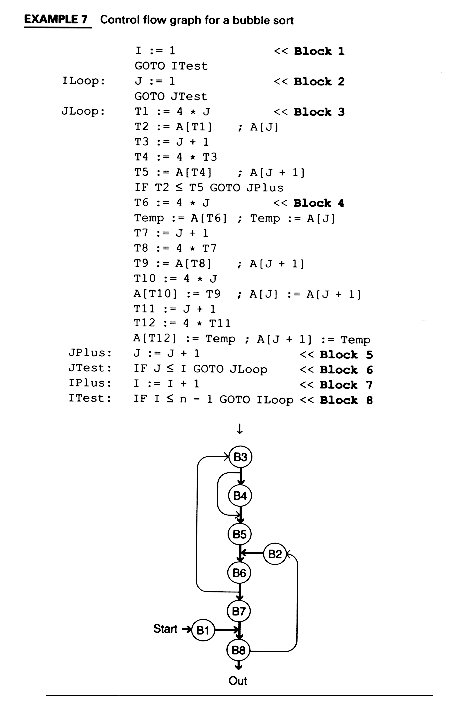
Example 8 shows a DAG for block 3 of Example 8.
The program of Example 7 contains cycles which may be loops. Determining loops is a major activity of control flow analysis. Creating basic blocks and a control flow graph are two steps toward this process. In the next section, we will formalize the process of determining a loop in a control flow graph.

Send questions and comments to: Karen Lemone
 I := 1
GOTO ITest
ILoop: J := 1
GOTO JTest
JLoop: T1 := 4 * J
T2 := A [T1] ; A[J]
T3 := J + 1
T4 := 4 * T3
T5 := A[T4] ; A[ J + 1 ]
IF T2 <= T5 GOTO JPlus
T6 := 4 * J
Temp := A[T6] ; Temp := A[J]
T7 := J + 1
T8 := 4 * T7
T9 := A[T8] ; A { J + 1 ]
T10 := 4 * J
A[T10] := T9 ; A[J] := A[ J + 1 ]
T11 := J + 1
T12 := 4 * T11
A[T12] := Temp ; A [ J + 1 ] := Temp
JPlus: J := J + 1
JTest: IF J < = I GOTO JLoop
IPlus: I := I + 1
ITest: IF I <= n - 1 GOTO ILoop
I := 1
GOTO ITest
ILoop: J := 1
GOTO JTest
JLoop: T1 := 4 * J
T2 := A [T1] ; A[J]
T3 := J + 1
T4 := 4 * T3
T5 := A[T4] ; A[ J + 1 ]
IF T2 <= T5 GOTO JPlus
T6 := 4 * J
Temp := A[T6] ; Temp := A[J]
T7 := J + 1
T8 := 4 * T7
T9 := A[T8] ; A { J + 1 ]
T10 := 4 * J
A[T10] := T9 ; A[J] := A[ J + 1 ]
T11 := J + 1
T12 := 4 * T11
A[T12] := Temp ; A [ J + 1 ] := Temp
JPlus: J := J + 1
JTest: IF J < = I GOTO JLoop
IPlus: I := I + 1
ITest: IF I <= n - 1 GOTO ILoop


