Lots of hashing functions have been developed for names (See Exercise 5 ). It has been joked that the hashing table for symbol tables is irrelevant as long as it keeps the variables I, N, and X distinct!
The hashing functions consist of finding a numerical value for the identifier, perhaps some combination of the ASCII code as a number or even its bit code, and then performing some of the techniques used for hashing numbers (taking the middle values, etc.).
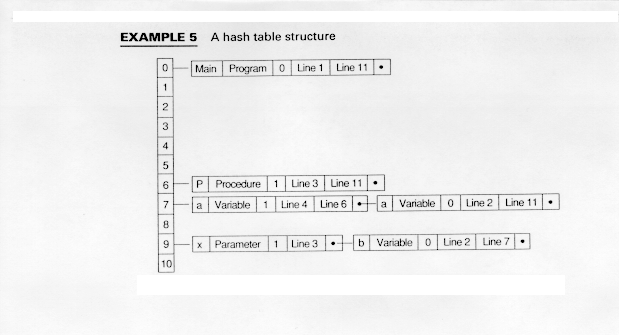
Example 5 creates a hash table using the formula

Notice in Example 5 that both instances of variable a have been hashed to the same position in the hash table and that both x and b have hashed to the same position.
If the hash function distributes the names uniformly, then hashing is very efficient - O(1) in the average case. The worst case, where all names has to the same number, has a time O(n). This case is unlikely, however.
More space is generally needed for a hash symbol table structure, so it is not as space-efficient as binary trees or list structures.
If new entries are added to the front of the linked structure, scoping is easily implemented in a single table. In fact, separate tables usually take up too much extra space.
