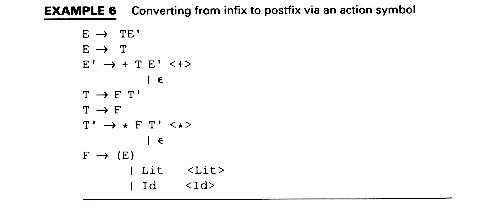
We illustrate action symbols using the notation "< >" which indicates that the symbol within the brackets is to be pushed onto the semantic stack when it appears at the top of the parse stack. By inserting this action in appropriate places, we will create a translator which converts from infix expressions to postfix expressions.


a b c * +
the input string translated to postfix. In Example 6, the action symbol did not have any attached attributes.
The BNF in Example 6 is in LL(1) form. This is necessary for the top-down parse.
The formal definition of an L-attributed grammars is as follows. An attribute grammar is L-attributed if and only if for each production X0 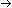 X1 X2. . . Xi. . . Xn,
X1 X2. . . Xi. . . Xn,
(1) {Xi.inh} = f ({Xj.inh} , {Xk.att}) i, j >= 1, 0<=k< i
(2) {X0.syn} = f ({X0.inh} , {Xj.att}) 1 <= j <= n
(3) {ActionSymbol.Syn} = f ({ActionSymbol.Inh})
(1) says that each inherited attribute of a symbol on the right-hand side depends only on inherited attributes of the right-hand side and arbitrary attributes of the symbols to the left of the given right-hand side symbol.
(2) says that each synthesized attributes of the left-hand-side symbol depends only on inherited attributes of that symbol and arbitrary attributes of right-hand-side symbols.
(2) says that the synthesized attributes of any action symbol depend only on the inherited attributes of the action symbol.
Conditions (1), (2), and (3) allow attributes to be evaluated in one left-to-right pass (see Exercise 2).
If the underlying grammar is LL(1), then an L-attributed grammar allows attributes to be evaluated while parsing. The reader may wish to review the LL(1) parsing driver in Chapter 4. The evaluation algorithm is:

For the next few sections, we focus on restrictions to attributes that allow for efficient attribute evaluation.
