4.1.2 Elimination of Left-Recursion

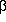
Step One: Direct-Recursion

For each rule which contains a left-recursive option,

A --> A |

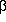
introduce a new nonterminal A' and rewrite the rule as

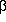A --> A'
A' --> | A'

Thus the production:

E --> E + T | T

is left-recursive with "E" playing the role of "A","+ T" playing the role of , and "T" playing the role of 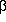A'. Introducing the new nonterminal E', the production can be replaced by:

E --> T E'
E' --> | + T E'

Of course, there may be more than one left-recursive part on the right-hand side. The general rule is to replace:

A --> A | | ... | | | ... |

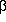
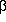
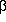
by

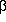
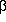
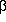
A --> A' | A'| ...| A'
A' --> | A' | A' | ...| A'

Note that this may change the "structure". For the expression above, the original grammar is left-associative, while the non-left recursive one is now right-associative.

Step Two: Indirect-Recursion

Step one describes a rule to eliminate direct left recursion from a production. To eliminate left-recursion from an entire grammar may be more difficult because of indirect left-recursion. For example,

A --> B x y | x

B --> C D

C --> A | c

D --> d

is indirectly recursive because
A ==> B x y ==> C D x y ==> A D x y.

That is, A ==> ... ==> A where is D x y.

The algorithm eliminates left-recursion entirely. It contains a "call" to a procedure which eliminates direct left-recursion (as described in step one).

Example 3 illustrates this algorithm for the grammar of Example 3.



Send questions and comment to: Karen Lemone