 is recognized by a nondeterministic
finite automaton that has no way to get to a final state.
is recognized by a nondeterministic
finite automaton that has no way to get to a final state.
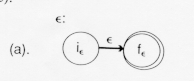
 is recognized by the nondeterministic
finite automaton which goes from its initial state to its final state
by reading no input. Such a move is called an
is recognized by the nondeterministic
finite automaton which goes from its initial state to its final state
by reading no input. Such a move is called an
 - transition
- transition
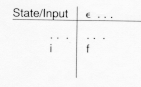
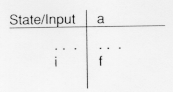
In table form this would be denoted:
 and how it would be
recognized by the driver. In fact, it will not be. This is just a first
step in table creation, and we will allow the creation of a
nondeterministic finite automation (NFA). Section
3.3.2 outlines how to turn this NFA into a deterministic finite
automation (DFA)
and how it would be
recognized by the driver. In fact, it will not be. This is just a first
step in table creation, and we will allow the creation of a
nondeterministic finite automation (NFA). Section
3.3.2 outlines how to turn this NFA into a deterministic finite
automation (DFA)
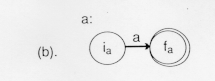
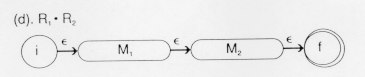
The diagram above shows that the language {a} denoted by the regular expression a is recognized by the finite automatation that goes from its initial to final state by reading an a. In table from this would be:
 and R
and R , respectively, are recognized by the finite automata
denoted by M
, respectively, are recognized by the finite automata
denoted by M and
M
and
M .
.
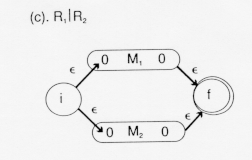
Adding  -transitions to the beginning and end creates a finite automation
which will recognize either the language represented by
R
-transitions to the beginning and end creates a finite automation
which will recognize either the language represented by
R or the language
represented by R
or the language
represented by R ,
i.e., the union of these two languages,
LR
,
i.e., the union of these two languages,
LR U LR
U LR .
.
We could eliminate the new final state and the  -transitions to it by
letting the final states of M
-transitions to it by
letting the final states of M and
M
and
M remain final states.
remain final states.
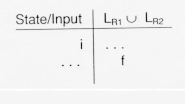
In table form, this is:
 or LR
or LR may lead to other intermediate
states.
may lead to other intermediate
states. Our example, which recognizes
Letters = A | B | C | . . . | a | b | . . . |z
and
Literal = 0 | 1 | 2 | . . . | 9
will use this step.
 is the machine that accepts LR
is the machine that accepts LR and M
and M is the language
that accepts LR
is the language
that accepts LR . Thus, after this combined automation has recognized a
legal string in LR
. Thus, after this combined automation has recognized a
legal string in LR , it will start looking for legal strings LR
, it will start looking for legal strings LR . This is
exactly the set of strings denoted by R
. This is
exactly the set of strings denoted by R
 R
R . The related table is:
. The related table is:
 upon recognition of strings in
LR
upon recognition of strings in
LR , then from the final state in
M
, then from the final state in
M ,
fM
,
fM to
the initial state in
M
to
the initial state in
M on an
on an  -transition, that is, without reading any
input, and then from the initial state in
M
-transition, that is, without reading any
input, and then from the initial state in
M ,
iM
,
iM to the final state in
M
to the final state in
M ,
fM
,
fM upon recognizing the strings in
LR
upon recognizing the strings in
LR .
The
.
The  is often omitted. It is understood that two regular expressions
appearing next to one another represents the concatenation.
We will use this step for the example, when we define an identifier as a
string of letters and digits (conatenated). Another example will recognize a
literal as the concatenation of one or more digits, that is,
is often omitted. It is understood that two regular expressions
appearing next to one another represents the concatenation.
We will use this step for the example, when we define an identifier as a
string of letters and digits (conatenated). Another example will recognize a
literal as the concatenation of one or more digits, that is,
Identifier = Letter (Letter | Digit) *
means
Identifier = Letter (letter | Digit) *
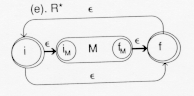
Here, M is a finite automation recognizing some LR. A new initial state is
added leading to both M and to a new final state. The
 - transition
recognizes the empty string,
- transition
recognizes the empty string,  (if R did not contain
(if R did not contain  already). The
transition to M causes the language LR to be recognized. The
already). The
transition to M causes the language LR to be recognized. The
 transition
from all final states of R to its initial state will allow the recognition
of LR
transition
from all final states of R to its initial state will allow the recognition
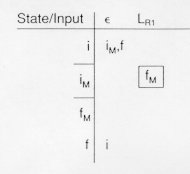
of LR , i = 1, 2,... The table is:
, i = 1, 2,... The table is:
We will use this step as well as the preceding two, for the regular expressions
Identifier = Letter (Letter | Digit)*
and
Literal = Digit* = Digit Digit*
Using these diagrams as guidelines, we can "build" a nondeterministic finite automation from any regular expression (See Exercise 6
Send questions and comment to: Karen Lemone