10.4 An Example

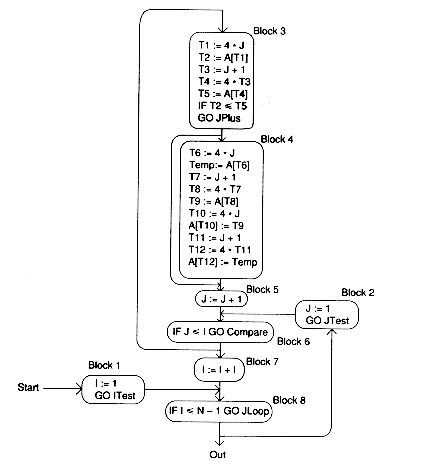
In this section, we perform an example which includes many of the optimizations discussed so far:

Consider the algorithm for a Bubblesort from Chapter 7:

	
FOR I := 1 TO N - 1 DO
  FOR J := 1 TO i DO
    IF A[J] > A[J + 1] THEN
      Temp := A[J]
      A[J] := A[J + 1]
    ENDIF
  ENDFOR
ENDFOR

The intermediate representation (shown as quadruples) and the control flow graph are:

One of the best optimizations here would be an algorithm optimization, which would replace Bubblesort with a better algorithm such as Quicksort. We won't do this however.

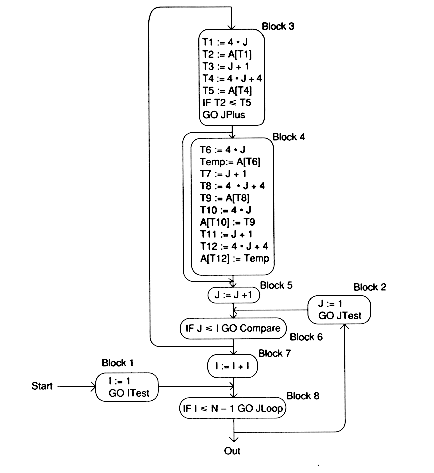
There are algebraic optimizations here: T4 computes 4 * T3 = 4 * (J + 1) = 4 * J + 4. Similarly, T8 computes 4 * T7 = 4 * ( J + 1) = 4 * J + 4 and T12 = 4 * T11 = 4 * (J + 1) = 4 * J + 4. Changing these:

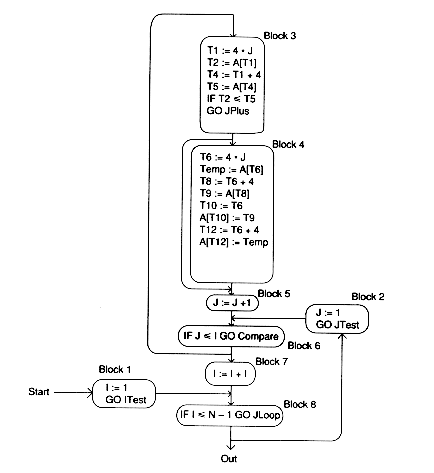
We look for some local optimizations which can be performed within the basic blocks.

There is local common subexpression elimination to be performed in our example. In Block 3, both T1 and T4 compute 4 * J. In Block 4, T6, T8, T10, and T12 compute 4 * J; both T7 and T11 compute J + 1; both T8 and T12 compute 4 * J + 4.

We will replace the second occurrence of 4 * J in Block 3 by its value, T1, and the second, third and fourth occurrence in Block 4 by the computed value T6, T3, T7, and T11 go away:

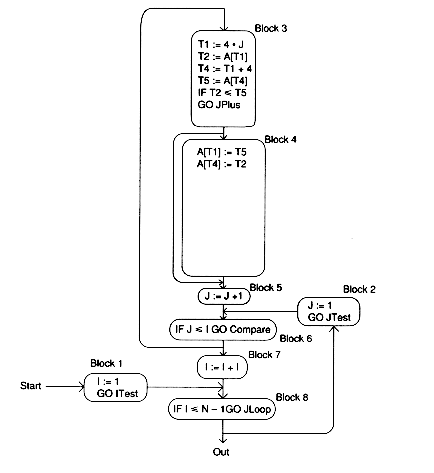
There is no opportunity for local constant folding or elimination unless n is known at compile time.

We move on to global and loop optimizations, presuming that data flow analysis has been performed (see Module 9, Exercise 2).

In Block 4, A[T6] which is A[4*J] is computed in Block 3. Control flow analysis tells us that we can't get to Block 4 without going through Block 3, and data flow analysis tells us that J doesn't change in between. Thus, we replace the first two statements in Block 4 by:

Temp := T2

Similarly, T10 is the same as T1, T8 is the same as T4, and T12 is the same as T4.

Block 4 becomes:

Temp := T1		 A[T1] := T5
A[T1] := T5		A[T4] := T1
A[T4] := Temp

Looking at the revised program:

Next, we find the natural loops in order to perform induction-variable elimination. It is somewhat difficult to find the header of the inner loop because of the way the control flow graph is drawn, but Block 6 satisfies the definition from Module 8 (the reader is invited to check this). The loops are {6,3,4,5} and {2,3,4,5,6,7,8}.

For the loop, {Block 6, Block 3, Block 4, Block 5}, there are induction variables J (incremented by 1) and T1 and T4 (incremented by 4)

In Block 3:

T1 = 4 * J
T4 = 4 * J + 4

We can eliminate J, replacing the test on J with one on T1:

IF J<= I		IF T1 <= 4 * I

Note that J cannot be eliminated if it is to be used later in the program.

The new Block 6 becomes:

T14 := 4 * I
IF T1 <= T14 GO JLoop

In Block2, we eliminate the initialization of J and replace it with a new Block 2:

T1 := 4
T4 := 8

Block 2 is functining as a preheader here. We also need to replace the increment of J by an increment of T1 and T4. The new code is:

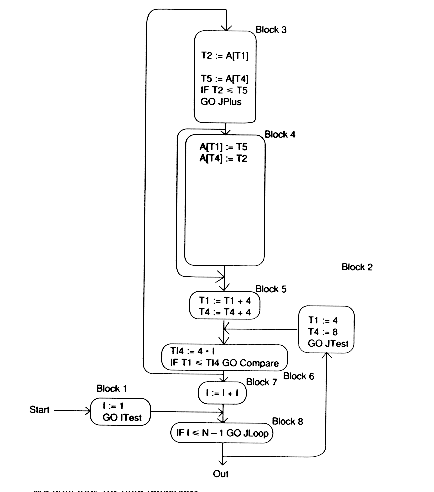
We new look for loop invariants .

T14 := 4 * I

is invariant in the inner loop, and we move it to Block 2:

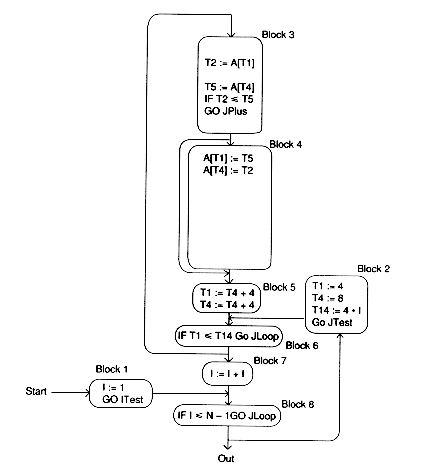
The final code is much improved over that shown originally. The reader is invited to search for more optimization to be performed here.