CS 2223 Apr 27 2023
Expected reading: pp. 638-657
Musical Selection:
Len: Steal My Sunshine (1999)
Visual Selection:
Ancient
of Days, William Blake (1757 - 1827)
Live Selection:
What a Wonderful World, Louis Armstrong (1967)
Jazz Selection: No Problem, Art Blakey and the Jazz Messengers (1959)
1 Single-Source Shortest Path
1.1 Class Climate and Online Student Course Reports
Here’s another way to tell the end of the term is approaching: In Canvas the Class Climate link is now active. It’s great that 11 students have already responded. Now comes the hard part, trying to get the response rate over 66%.
I know that we are all busy, especially this time of year. This survey only takes a few minutes to complete and I will now mention it every day, and every chance I can whe interacting with students. I find this feedback extremely useful when I sit down and evaluate what to do next year.
This year I have added a single, optional "Instructor’s Question" where I’m hoping to get some ideas to increase student engagement.
You have until Thursday May 4th to complete and I hope you take the time to complete one!
1.2 Variations on SSSP
We now have an algorithm for computing the single-source, shortest path within a weighted, directed graph containing non-negative weights. With the code shown yesterday, the performance is classified as O((V+E) * log V). The book (proposition R on page 654) shortens this to O(E log V) in the worst case. This can be done because E is the dominant value when compared with V.
What if you instead implement the Digraph using an AdjacencyMatrix. What changes with regards to the code, and possibly, the overall performance.
1.3 AdjacencyMatrix representation
An Adjacency matrix representation creates a two-dimensional array which stores the potential edge weights.
public class DigraphAdjacencyMatrix extends EdgeWeightedDigraph{ double[][] weights; public DigraphAdjacencyMatrix (int V) { super(V); weights = new double[V][V]; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { weights[i][j] = Double.NEGATIVE_INFINITY; } } } ... }
We have some choices for specifying "no-edge". One idea is to use an edge weight of "0" for that purpose. Still, we might find ourselves with a graph in which we might allow edge-weights of 0, so we choose to declare a non-existent edge with Double.NEGATIVE_INFINITY.
This representation is unable to determine all adjacent vertices without checking through all possible candidates, thus:
public Iterable<DirectedEdge> adj(int v) { Queue<DirectedEdge> queue = new Queue<DirectedEdge>(); for (int i = 0; i < V; i++) { if (weights[v][i] != Double.NEGATIVE_INFINITY) { queue.enqueue(getEdge(v,i)); } } return queue; }
The reason this becomes a problem for the algorithms we are discussing is that we have been making a common assumption regarding performance of the following code:
for (int u = 0; u < g.V(); u++) { for (int v : g.adj(u)) { statement } }
Earlier this week, I argued that the above code executes statement E times for directed graphs and 2E times for undirected graphs.
Now, however, with an adjacency matrix, the above code will require time that is directly proportional to V2, since the outer u loop executes V times, and each pass through g.adj(u) requires V times as well.
Even worse, the above code is wasteful in that it constructs a queue to contain all edges, when in fact you would do better to optimize the DijkstraSP code to work directly off of a 2D array.
N #Edges Time-List Time-Matrix 128 3246 0.000000 0.000000 256 13091 0.000000 0.000000 512 52209 0.000000 0.016000 1024 209471 0.015000 0.000000 2048 838639 0.000000 0.047000 4096 3354546 0.031000 0.171000 8192 13421744 0.156000 3.229000
Using the small example code CompareDensePerformance, the performance is 20x slower with matrix representation.
1.4 Variations on Single-Source Shortest Path
There are several variations that might be considered (p. 654).
1.4.1 Undirected graphs
This is an example in computer science of reducing one problem to another problem for which we already have a solution.
Hint: Use this approach for one of the questions on HW4.
1.4.2 Directed Acyclic Graphs
What if you know the graph is a DAG, that is, there are no cycles? A more efficient variation of Dijkstra’s SP algorithm (page 658) is to relax the vertices in topological sort order. Since you know there are no cycles, each edge is going to be visited exactly once. This approach doesn’t need to use a priority queue, which means its performance is based on the performance of Topological Sort (p. 583) which means the worst case is O(E + V). This is a noticeable improvement over O(E*log V).
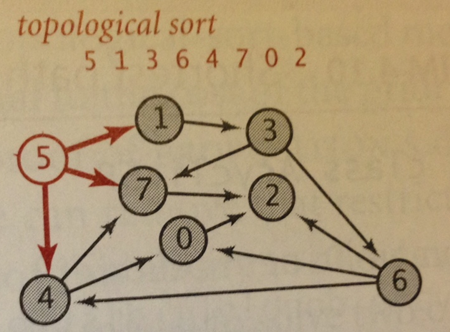
Here is a sketch of the algorithm. Once the topological order is computed, you process each vertex in order, relaxing all edges from those vertices. Note there is no need to use a priority queue because you rely on the topological sort to give you the vertices in a proper order; certainly, you might find a better shortest path with more edges, which forces a relax operation, but this won’t affect the order in which you process the vertices.
// Relax without a priority queue since Acyclic void relax (EdgeWeightedGraph G, int v) { for (DirectedEdge e : G.adj(v) { int w = e.to(); if (dist[w] > dist[v] + e.weight()) { distTo[w] = dist[v] + e.weight(); edgeTo[w] = e; } } } void shortestPath(EdgeWeightedGraph G, int s) { Topological top = new Topological(G); // Process each vertex in order for (int v : top.order()) { relax (G,v); } }
1.4.3 Negative Edge Weights
What if we wanted to allow edge weights to be negative. This fundamentally alters the nature of the problem.
Note that Dijkstra’s SP algorithm used a priority queue to determine the order of vertices to investigate. And the claim was that the vertices removed from the priority queue were done in shortest distance from the source. This claim was made possible because successive paths only increased the total distance, so now our original assumption is invalid.
Consider the following small graph:
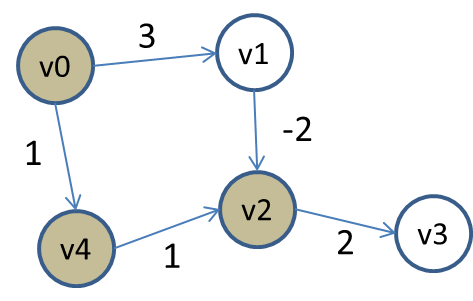
The vertices are colored based on whether they have been processed and removed from the priority queue. As usual, we compute Single-Source Shortest path starting from vertex v0. All vertices in the priority queue have INFINITY as distance (except for v0 which is the source). After removing v0, it updates the distances for v1 and v4 because of the existing edges to those vertices. Now, v4 is the first to be removed, since its total distance is 1, placing it at the "top" of the priority queue, which vertex v1 has distance of 3, placing it second. Once v4 is removed, the edge to v2 relaxes that distance.
Thus vertex v2 is adjusted (that is, decreaseKey is called) and the priority queue contains three vertices with the following distance (aka, priorities):
v2 with distance 2
v1 with distance 3
v3 with distance INFINITY
Naturally, it removes v2 from the priority queue and eventually v3 is adjusted with a total distance/priority of 4.
As you can see, Dijsktra’s SP algorithm just "assumes" that any edge coming from v1 to v2 will only increase the total accumulated weight, however, when removing v1 from the priority queue (since it is the lowest distance), it suddenly sees an opportunity to reduce the total distance to v2.
However v2 has been removed from the priority queue and so it can’t be relaxed. In fact, if you try to do this, the code will throw an exception. You could choose to "mask" this exceptional case, by modifying the DijkstraSP code as follows:
void relax(DirectedEdge e) { int v = e.from(); int w = e.to(); // distance from s ->v + edge weight (v, w) < distance from s to w if (distTo[w] > distTo[v] + e.weight()) { distTo[w] = distTo[v] + e.weight(); edgeTo[w] = e; if (pq.contains(w)) { pq.decreaseKey(w, distTo[w]); } } }
And this would work for a little while... but it won’t last.
There is one more awkward situation to deal with. What if there is a negative cycle, that is, a directed cycle whose total weight (sum of the weights of the edges) is negative. If such a cycle existed, one could arbitrarily lower the total path cost by simply iterating through thus cycle as many times as you would like. So we must find a way to detect negative cycles in any graph that allows negative weights.
1.5 Bellman-Ford Algorithm
The book describes Bellman-Ford in a way that is more complicated than it needs to be. Bellman-Ford has the same approach that Dijkstra’s has, namely, find some edge to relax (or lower) distance. However, instead of trying to find vertices from which we relax individual edges, Bellman-Ford processes all edges within a fixed number of iterations.
int n = G.V(); for (int i = 1; i <= n; i++) { // for each edge in the graph, see if we can relax for (DirectedEdge e : G.edges()) { if (relax(e)) { if (i == n) { return; // negative cycle. DONE } } } }
And here is the relaxation code, as expected. For convenience, it returns true if the edge reduces the best shortest path.
boolean relax(DirectedEdge e) { int v = e.from(); int w = e.to(); if (distTo[w] > distTo[v] + e.weight()) { distTo[w] = distTo[v] + e.weight(); edgeTo[w] = e; return true; } return false; }
The best part of Bellman-Ford is that you don’t need to check for negative cycles. In each iteration (there are N of them where N=V) you process all edges to see if you can relax the distance. If you make a full pass over all the edges and you did not find a single edge to relax, then you know that you are done.
Let’s analyze the performance of this code. The outer for loop executes V time, and the inner for loop executes E times, thus the performance of this code is Θ(E*V).
However, what if you keep making iterations, and keep finding edges that seem to relax a distance, here and there. How do you know if you are still making progress to the actual solution? It turns out there is a very simple answer to this question.
I’ll start by asking this: What is the longest possible path between any two vertices in a directed weighted graph? Well, if there are V vertices, then it must be V-1 edges.
So, thinking along the lines of breadth first search, if you start at a source and complete one iteration over all edges, you know that you have the shortest distance between source and all vertices one edge away. After the second iteration, you know that you have the shortest distance between source all all vertices two (or fewer) edges away. If you continue through V-1 iterations, you will have completed the solution.
However, what if a negative cycle exists? Well, then go ahead and iterate one more time, and if you find an edge that relaxes a distance value, you know there must be a negative cycle.
This is why the for loop iterates exactly V times.
There is also a nice optimization here. It may turn out that after a few iterations, you find no other edge that can be relaxed. In this case, perhaps long before V, you can stop and declare a solution.
If you look at the code, you will see how we handle these two edge cases.
1.6 All Pairs Shortest Path
Instead of finding the shortest path from a single source, we often seek the shortest path between any two verices (u, v). There may be several paths with the same total distance. The fastest solution to this problem uses a technique known as Dynamic Programming.
There are two interesting features of dynamic programming:
It stores the solution to small, constrained versions of the problem
In addition to finding the optimal answer, you also want to be able to recover the paths themselves. So we need to store additional information to make this happen.
The Floyd-Warshall algorithm computes an n-by-n matrix dist such that for all pairs of vertices, u and v, dist[u][v] contains the length of a shortest path from u to v. The input to the algorithm is a directed, weighted graph G = (V,E). Each edge e=(u,v) has an associated positive weight (i.e., > 0).
It works by computing the dist[][] matrix which represents the shortest distance from each vertex u to every other vertex in the graph (including itself). Note that if dist[u][v] = INFINITY then there is no path from u to v. The actual shortest path between any two vertices can be computed from a second matrix, pred[][], also computed by the algorithm.
// pred[u][v] means "on shortest path from u to v, // last edge came from vertex pred[u][v]." pred = new int[G.V()][G.V()]; dist = new double[G.V()][G.V()]; // initialize edges and base cases for (int u = 0; u < G.V(); u++) { for (int v = 0; v < G.V(); v++) { dist[u][v] = Integer.MAX_VALUE; pred[u][v] = -1; } dist[u][u] = 0; // distance to self is 0 for (DirectedEdge edge : G.adj(u)) { int v = edge.to(); dist[u][v] = edge.weight(); pred[u][v] = u; // base case } } // algorithm now proceeds for (int k = 0; k < G.V(); k++) { for (int u = 0; u < G.V(); u++) { for (int v = 0; v < G.V(); v++) { // can we shorten distance from u to v by going through k. double newLen = dist[u][k] + dist[k][v]; if (newLen < dist[u][v]) { dist[u][v] = newLen; pred[u][v] = pred[k][v]; // TRICK: } } } }
The key insight of this algorithm is the outermost for loop on k.
We make a full sweep through all (u,v) pairs and ask the question: "Can you improve the distance from u to v by trying to go from u to k, and then from k to v?"
As k increases, you eventually try out every possible improvement and ultimately compute the final result. Let’s see this in action:

The above figure represents dist[u][v] and asks the repeated question, "can you outperform dist[u][v] by seeing if there is a shorter path from u to k and then from k to v. No longer (like Dijkstra’s Single Source Shortest Path) are we restricted to finding an edge (u,v) from which we improve the distance from s to v by going throught u. Here you are incrementally finding whether there is "a better path from u to v by finding paths that go through vertices 0, then {0, 1}, and then {0, 1, 2} and so on. Until all possibilities have been exhausted.
In addition to dist[][], Floyd Warshall also computes pred[u][v] which is the "vertex on the last edge of the shortest path from u to v." For this example above, pred is the following:
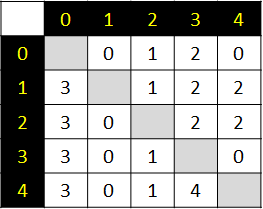
This 2d matrix has no intuitive explanation, until you work out these shortest paths, as shown below, and then it should make sense:

1.7 Time Classification
How would you classify the run-time performance of FloydWarshall? Review the code above and you will see that the primary triply nested for-loop will leads to a classification of O(V3). What about the initialization for-loops? You can see that V2 matrix values are initialized. Then each of the directed edges is visited once in the graph; the initialization is thus O(V2 + E). Altogether, the V3 term dominates, resulting in a total performance classification of O(V3).
Perhaps this isn’t the most efficient solution to the problem. What if we chained together the results of V executions of Dijsktra’s single-source shortest path algorithm? That is, for each vertex, vi execute DijkstraSP(vi). We already know from yesterday that its performance is classified as O((V+E) * log V). So the performance of Chained-Dijkstra-SP – running Dijkstra-SP V times – is O(V * (V+E) * log V).
How do we decide which one to pursue?
Well, for sparse graphs, E is on the order of V (for example, no more than 5*V or some fixed constant). In this case, Chained-Dijkstra-SP would be considered O(V * (V + 5*V) * log V) which is O(V * 6V * log V) and this is O(V2 * log V). This is the clear winner.
However, for dense graphs, E is on the order of V2 (for example, V*(V-1)/4). In this case, Chained-Dijkstra-SP would considered O(V * (V + V*(V-1)/4) * log V) which is O((V*V + V*V*(V-1)/4) * log V) or O(V3 * log V) which would then be outperformed by Floyd Warshall.
I put together a sample program, Compare which demonstrates the side-by-side comparison of these two approaches on random graphs where the number of edges hits the "break-even point". I compute this by considering when:
V3 ~ V*(V+E)*log V.
When E is on the order of V2/log V, you should be able to see that the right-hand side becomes V*V*log V + V*(V*V/log V)*log V which approximates V3. Do not look at these as the equality of two functions – rather, this is where the classification families "overlap".
Here is the output for break-even graphs:
V E time FW time Chained-Dijsktra 16 34 0.0156001 0.0 32 106 0.0 0.0 64 324 0.0 0.0156 128 1107 0.0156 0.0156 256 4077 0.0156 0.0936 512 14705 0.1560 0.1872 1024 52272 1.1232 1.2480 2048 190215 8.5020 10.6860
For dense graphs (i.e., when p = 0.5) the results are noticeably different:
V E time FW time Chained-Dijsktra 16 131 0.0 0.0156 32 517 0.0 0.0 64 2104 0.0 0.0156 128 8121 0.0 0.0624 256 32794 0.0156 0.1560 512 131266 0.1404 1.6692 1024 524532 1.2012 13.7904 2048 2097089 9.4068 123.9583
This completes treatment of graphs. There are many other problems of interest on graphs – many of them are described in the textbook.
1.8 Big Theta Notation
Can you explain why "T(n) = N - 999" is classified as Θ(N).
Try to find c1 such that for all N > n0, c1*N < N - 999.
Now try to find c2 such that for all N > n0, c2*N > N - 999.
If you can find these three constants (c1, c2 and n0) then you can claim that T(n) is Θ(N).
1.9 Version : 2023/04/28
(c) 2023, George T. Heineman
