CS 2223 Apr 04 2023

Lecture Path: 13
Back Next

Exam 1 is to be held Thursday
Classical selection: Samuel Barber: Adagio For Strings (1936)

Visual Selection:

Musical Selection: Tracy Chapman: Fast Car (1988)
Visual Selection: Aficionado, Georges Braque (1912)
Live Selection: Creep, Radiohead (1994)
Jazz Selection: I Wish I Knew How it Would Feel to Be Free, Nina Simone (1976)

1 Preparing for Exam 1

I will complete the lecture on maintaining a heap for priority queues today if I did not complete from yesterday.

Then determine its running time by computing order of growth, or Big O, based on the size of the array, N.

1.1 Fundamental Concepts

There are no secrets to success. It is the result of preparation, hard work learning from failure.

General Colin Powell

Brief review of the first half of this course, and fundamentals we have been practicing.

We have worked extensively with arrays (on HW1) .

One dimensional arrays have nice search behavior when the values are in sorted order, since you can use BinaryArraySearch to locate a value in the array in floor(log N) + 1 array inspections/comparisons.

This is a fundamental fact we have used a number of times.

What if you had a square matrix?

int n = a.length; // Square n x n matrix for (int r = 0; r < n; r++) { for (int c = 0; c < n; c++) { if (a[r][c] == target) { return true; } } }

This would require n x n comparisons.

Sometimes a two-dimensional arrays is lower-triangular, that is there are N rows and N columns, but not all entries were used. Accessing these made a small modification to the for loop:

int n = a.length; // find number of rows for (int r = 0; r < n; r++) { for (int c = 0; c <= r; c++) { if (a[r][c] == target) { return true; } } }

For a given 4x4 matrix:

2 0 0 0 3 1 0 0 6 7 3 0 8 9 1 2

you had to check a total of 1 + 2 + 3 + 4 = 10 comparisons.

Given what you know of triangular numbers, this is 4*5/2, which in general would be n*(n+1)/2.

You are now aware of the five fundamental data types

Bag (p. 121) – Use with collections of non-comparable objects. Use when you don’t care overmuch about individual retrieval of elements but rather only want to retrieve all elements one at a time.
Stack (p. 121) – Use when you want Last-in, First-out (LIFO) behavior. Can be structured to support expandable collections or can be restricted to fixed capacity.
Queue (p. 121) – Use when you want First-in, First-out (FIFO) behavior. Can be structured to support expandable collections or can be restricted to fixed capacity.
Max Priority Queue (p. 309) – Use when you want to retrieve specific element that is "largest value" or "highest priority". Can be structured to support expandable collections or can be restricted to fixed capacity.
Symbol Table (p. 363) – Use when you want to associate a value with a key.

Note that the Max Priority queue can be augmented to support arbitrary re-classification of "value" or "priority" (IndexMinPQ (p. 320) which we will cover in few weeks). No need to know about indexMinPQ for exam tomorrow.

You should know how stacks and queues can both be implemented using arrays or linked lists.

We covered how using arrays would work for a fixed queue of size N, effectively implementing a circular buffer.

1.2 Recurrence Relations

You have seen these in lecture a number of times. They appear, for example, as follows, in many of the divide and conquer algorithms:

Entire Lecture Mar 27 2023
Daily Exercise, Mar 24 2023
MergeSort (p. 272)

What matters is how you identify the operation being counted, and how you set up the equations.

Let’s try a past exam question:

static int process(int[] a, int lo, int hi) { if (lo == hi) { return (int) Math.sqrt(a[lo]); } int mid = lo + (hi-lo)/2; int x = process(a, lo, mid) + process(a, mid+1, hi); for (int i = lo; i <= hi; i += 2) { if (Math.sqrt(a[i]) == x) { x++; } } return x; }

If you are counting the number of times Math.sqrt is executed when invoked on an array of size N=2n, then the equation is:

S(1) = 1 (Base Case)

S(N) = S(N/2) + S(N/2) + N/2

since the for loop will execute N/2 times because i is incremented by 2 with each pass.

S(N) = 2*S(N/2) + N/2 and then you work out as we did in past lectures:

S(N) = 2*[2*S(N/4) + N/4] + N/2

S(N) = 2*[2*[2*S(N/8) + N/8] + N/4] + N/2

Regroup to find:

S(N) = 23*S(N/23) + 3*N/2

How many times can you subdivide N by 2? Exactly k = Log N times, which produces:

S(N) = 2k*S(N/2k) + k*N/2

But you know S(N/2n) is S(1) which means this is 1.

S(N) = 2k + k*N/2

and replace log N for k you get:

S(N) = N + log(N)*N/2

1.3 Worst Case Analysis

We have focused our attention on counting the number of times a key operation is executed within an algorithm solving a problem of size N, where N is typically a power of 2.

Sometimes we can exactly determine the number of times an operation is called, much like L(n) above for Selection Sort.

Sometimes we can only bound it "above" and "below" using Best Case and Worst Case assumptions.

public static void sort(Comparable[] a) { int N = a.length; for (int i = 0; i < N; i++) { for (int j = i; j > 0 && less(a[j], a[j-1]); j−−) { exch(a, j, j-1); } } }

When it comes to Insertion Sort, how many times does less get called?

L(1) = 0, since the inner for loop never executes. For larger values of N, the inner loop will execute, but how many times?

L(N) = ... + L(N-1)

To determine how many times less is called, you have to consider the best case (the numbers are already in sorted order) or worst case (numbers are in reverse sorted order). In the worst case, the inner for loop executes i times, as i increases from 0 to N-1. We only need to consider cases where N > 1, since base case is handled earlier.

L(N) <= 1 + L(N-1) <= 1 + [2 + L(N-2)] <= 1 + [2 + [3 + L(N-3)]] <= 1 + 2 + 3 + L(N-3)

These are all "<=" because that is worst case analysis. How many times can you subtract 1 from N? N-1 times, so we have:

L(N) <= 1 + 2 + ... + N-1 + L(N-(N-1)) <= TN-1 +L(1) <= N*(N-1)/2

In the BEST case, you would only do one invocation to less, and thus this would be:

L(N) >= 1 + L(N-1) >= 1 + [1 + L(N-2)] >= 2 + [1 + [ + L(N-3)]] >= 1 + 1 + 1 + L(N-3) >= 1 + 1 + 1 + ... + 1 + L(N-(N-1))

Here, you would add 1 N-1 times, and so in the best case, only N-1 less comparisons are required.

Thus you know the actual number of invocations of less is defined as:

N-1 <= L(N) <= N*(N-1)/2

1.4 Working with Linear Probing

Assume you have a LinearProbingST of size 10 that does not support resizing. In the image below, M=10. Also, as is typical, I am not interested in the values that are associated with the keys.

Figure 1: Linear Probing Array

What happens when inserting integer keys into this structure? Note that the hashCode() for an integer is simply the value itself. Next, recall that the hash() method must reduce this hashCode() value further, by computing "% M", or in this case "% 10", which results in values from 0 to 9. For example, the key 34 would have a hash() value of 4.

What is the resulting array after inserting the following keys into this structure: 34, 19, 15, 39, 8, 14, 28?

Figure 2: Linear Probing Result

1.5 Working with Heaps by example

The Heap as introduced yesterday had this structure:

public class Heap { int[] pq; // Store in pq[1..N] int N; // number of items in heap public Heap (int capacity) { pq = new int[capacity + 1]; } ... }

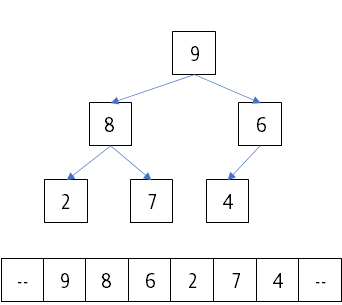
Assume you create heap = new Heap(7) and call insert() with the following values in this order: 2, 7, 4, 9, 8, and 6. Once all values are inserted, draw the tree representation of the final heap. Also show the array representation of pq that stores its values.

Figure 3: Heap Constructed

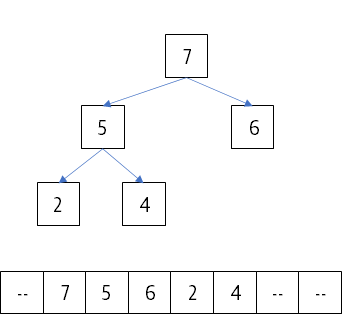
Based on the heap from above, call delMax() twice and then insert() the value 5. Draw the tree representation of the final heap. Also show the array representation of pq that stores its values.

Figure 4: Heap that results

1.6 Exam 1 Thursday

Exams are closed-book, closed-notes.

You may bring in one sheet of notes (one paper, 8.5" x 11.5", both sides) to each exam. This piece of paper must be handwritten and not printed.