CS 2223 Mar 16 2023

Lecture Path: 03
Back Next

Expected reading: pp. 96-99 (Designing Abstract Data Types, Section 1.2), 121-129 (Section 1.3)
Assume you know: pp. 64-89 (Section 1.2)
Lecture Challenges: Permutation strategies, Special Number

Visual Selection:

Classical selection: Grieg Piano Concerto in A major (1868)
Musical Selection: Barracuda, Heart (1977)
Visual Selection: Melencolia I, Albrecht Durer (1514)
Live Selection: Hound Dog, Elvis Presley (1956)
Jazz Selection: So What, Miles Davis (1959)

1 Well Begun Is Half Done

I’ve added an example to the day03 package in the code repository that shows how you can perform Binary Array Search over values stored in a TwoDimensionalStorage object (which you will use on the homework).

Find it PracticeWithTwoDimensionalStorage. See if you can extend it to locate values that are stored in an N-row, 1-column two-dimensional storage.

Also note that I’ve revised the rubrics for HW1 (so please review) and made small corrections to HW1 to clarify some points.

Finally, I’ve now modified my code for Q2 so that it prints out the actual Embedded Rectangle (or Permutation Array) if your result is incorrect. Hopefully this will help you debug your code better.

REALLY Finally, I have to move my Thursday office hours to 3PM today and they will be held in Beckett Conference Room, FL 246. Sorry for the hassle.

OK, NOW I AM PUSHING IT. Why Candy Crush? Why Now?

Figure 1: Candy Crush

1.1 Important concepts from readings

Today I asked you to read about three fundamental data types in computer science. These are Bag, Stack and Queue. Two of these (Stack and Queue) are already implemented by the JDK (as class java.util.Stack and interface java.util.Queue). You need to understand the interfaces for all three data types. You need to understand the choices you make when implementing them.

For the homeworks in this CS 2223 course, you should not use any of the java.util.* framework classes to complete the assignments. This will be increasingly important, especially in HW2, because I am asking you to learn how to structure data on your own, without taking advantage of fully-formed classes that essentially solve the problem for you.

1.2 Opening Questions

Wirth’s Law: Software is getting slower more rapidly than hardware becomes faster.
Nicholas Wirth

First let’s complete the accurate accounting to find the greatest and second greatest elements in a collection of N elements. Given just a small sample, you can see the following:

Size	Number Operations
2	1
3	3
4	4
7	8
8	9

Find top two values in n + ceiling(log(n)) - 2

If you reflect on the bracketology ideas I introduced, you can see that it still takes n-1 number of comparisons to locate the winner. Along the way you have derived useful information to help find the second largest. It can only be on the "path" of the tournament from the winner down to its first position. Given N elements, the height will be ceiling(log n), that is, the smallest integer larger than or equal to the real number of the computation log N. If we start with the final two teams in the tournament as our "#1" and "#2" then we only need to check ceiling(log(n)) - 1 numbers to find the second largest. Thus the maximum number of comparisons to find the top two numbers is n-1+ceiling(log(n))-1 or n + ceiling(log(n)) - 2.

The original code for the Apollo-11 program is available. It contains a routine that sorts three values.

Let’s start with the question I asked you to consider last lecture:

What is the fewest number of comparisons to sort five elements?

Here is my solution. Discuss.

Isn’t it interesting that you need 7 comparisons to completely sort all five elements but using this approach you need 6 comparisons to find the largest and second largest?

What do you make of the observation that 5 + ceiling(log(5)) - 2 = 6?

Well, using the tournament algorithm I mentioned yesterday, you can find the top two values from an array of FIVE values with n + ceiling(log(n)) - 2 = 6 comparisons, but I could sort these five values in just seven comparisons.

This question is of interest theoretically because we still don’t know the fewest number of comparisons to sort sixteen elements. Latest research from 2011 confirms that 46 comparisons suffices and that 44 do not. You would make international news if you could prove that 45 comparisons sufficed. Find the table of best comparison results on Wikipedia.

1.3 Data Types

The famous computer scientist Nicklaus Wirth published an influential book called "Algorithms + Data Structures = Programs (1978)." You need to understand these fundamental data types so you will be ready to tackle the more advanced ones later in this course.

Operation	Bag	Queue	Stack
add	add(Item)	enqueue(Item)	push(Item)
remove	--	dequeue()	pop()
size	size()	size()	size()
isEmpty	isEmpty()	isEmpty()	isEmpty()

We will look at each of these types in turn, as well as the fundamental core API. The notion of an API is found in the discussion from page 96-99. Here are the hilights:

These data types were designed to support well-defined behaviors but they also reflect common real-world scenarios. A Queue, for example, is a good way to model a line waiting to order food in the cafeteria. If you are first in line, you get to order before everyone else behind you. A Stack can represent the trays in a cafeteria that are in a pile of trays when you enter the cafeteria: You grab the topmost tray, which was the last one placed there.

Finally a Bag might represent the coins in the cash register. When the cashier wants to grab a quarter, they just grab one at random from the bin containing all quarters, without paying attention to the order in which the quarters had been added to the bin.

Note that these operations mutate the state of the data type in place.

We will be sure to separate discussions of a Data Type from implementation discussions of a Data Structure. Specifically, a Data Type has behavior made visible through an API while a structure represents the (seemingly arbitrary way) in which data is stored in memory.

1.3.1 Encapsulation

A well-designed data type does not reveal its implementation, because that is irrelevant to the outside world. It is kept private and hidden. That said, it will always reveal (explicitly or not) its performance, which can be documented. The fundamental principle is to describe the time it takes to perform an operation in relation to the problem size N. We started this discussion on Mar 14 2023 and we will be prepared to complete on Mar 17 2023.

This relates to material found on page 172-177.

1.3.2 Design APIs

A data type is defined by the behavior that it supports. In this regard, an array is not a data type but is a fundamental data structure, much like an int represents 32-bit integers while a long represents 64-bit integers.

Page 97 of the book lists a number of pitfalls when designing the interface to a data type. In many ways, this is an engineering problem, and most people can recognize a well-designed interface when trying to use it for the first time.

We will aim for the following attributes when designing data type interfaces:

consistency – naming across different types
completness – there are no missing methods
testability – satisfactorily validate the correctness of a data type only from its public specification
empirical validation – devise performance benchmarks to validate the timing specification of API functions.

1.4 FixedCapacityStack implementation

Pay special attention to the toString method that can be used while debugging.

Present implementation (as found in repository as FixedCapacityStack).

1.5 Dijkstra’s Two-Stack Algorithm

This algorithm on page 129 uses two stacks to process infix expressions with parentheses.

How do you solve problem "(1 + ((2+3) * (4*5)))"? Observe behavior and discuss.

You must walk through the trace on page 130-131 to verify you see how this algorithm works. On the homework you will see where it breaks down.

Sample Exam Question:

There is an alternate notation known as postfix notation. The above equation would be represented as "1 4 5 * 2 3 + * +". As its name implies, in postfix notation the operator comes after the arguments. Based on the structure of Dijkstra’s algorithm, devise a one stack solution to compute the value of this sequence of tokens.

On the exam, I would ask you to describe this algorithm using pseudocode, which we will be ready to discuss starting Monday.

Note that this is a practical problem. Have you heard of "Postscript"? This is the underyling notation for high-quality documents that, today, are known as PDF documents.

1.6 Stacks appear in many places

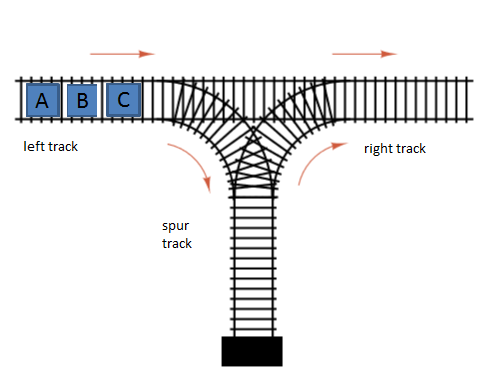
There are three engines on the left "A B C" in that order from left to right. You can move an engine straight through to the right track or it can move onto the spur track. Once on the spur track, the engine can only move onto the right track.

Figure 2: Track Manipulation

What is the only permutation of these three engines that you cannot reproduce on the right track?

1.7 Lecture Takeaways

Office hours are both held in person and online using Zoom. Check Canvas to see whether a particular office hour is in person or remote.
Homework 1 is now published.
We are working our way up to a cost model for algorithms. For starters, we will assume all basic operations can be performed in constant time. We are concerned with counting loops. We are concerned with operations whose performance depends on the size of a data structure.
Heineman evening online office hours available three-times, Sun/Tue/Thur at 7:30 pm

1.8 Lecture Challenges

Imagine if you wanted to create a FixedCapacityStack of up to 63 bits, where you could push values 0 or 1, and pop off the most recently pushed bit. Can you come up with an efficient structure and provide an implementation of the Stack API as described earlier?