CS 2223 Apr 28 2022

Lecture Path: 25
Back Next

Expected reading:
Daily Exercise:
Classical selection: Schubert: Symphony No. 5 in B-flat major, D. 485 (1816)

Visual Selection:

Musical Selection: Barenaked Ladies: One Week (1998)

Visual Selection: Christina’s World, Andrew Wyeth (1948)

Live Selection: People Time, Stan Getz and Kenny Barron (1991)

Daily Question: DAY25

1 Weighted graphs

1.1 Directed Weighted Edge

The final extension to the graph structure is assigning numeric weights to each edge. These weights represent various real-world measurements, such as distance, time, or cost.

Associating a weight is nothing more than constructing a structure to keep track of the source and target vertices and the edge weight:

public class DirectedEdge { final int v; final int w; final double weight; public DirectedEdge(int v, int w, double weight) { this.v = v; this.w = w; this.weight = weight; } public int from() { return v; } // Tail vertex of edge public int to() { return w; } // Head vertex of edge public double weight() { return weight; } // Weight of edge /** String representation. */ public String toString() { return v + "->" + w + " " + String.format("%5.2f", vweight); } }

How does this change the landscape? Well, consider the following graph:

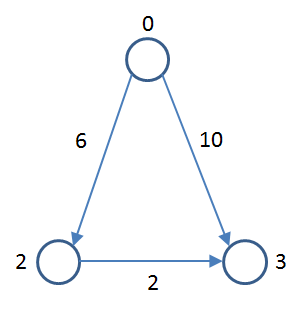
If you explore this graph using a Breadth First Strategy, you will see that you can get from vertex 0 to vertex 3 in one edge of weight 10, but if you traverse 0-2-3 over two edges, the accumulated length is 8 which is a shorter path.

We can’t use Depth First Search to find the shortest path. Using Breadth First Search would give the shortest path by total number of edges but not accumulated weight. Clearly we need some other strategy. Let’s be precise:

We want to compute the shortest possible accumulated path from a designated source vertex to each other vertex in G reachable from s.
We want to be able to recover these paths as needed.

To guide us in our search, reflect on a simple strategy that you used intuitively on the simple graph: Take action when your current shortest path calculation of s to t is larger than the sum of the distance from s to some vertex x plus the sum of the distance from x to t. To make this work you need to store extra information, but what should it be?

Consider how Breadth First Search constructed an array distTo[v] that recorded the shortest number of edges to traverse from vertex s to vertex v. In our case, use an array dist[v] that records our best computed shortest path from s to each vertex v. You can initialize this array to Infinity for all vertices, other than s which is set to 0.

This is half of the situation. However how can we find some vertex t which grants us a shorter path s-t-v for any vertex v? The answer is to be disciplined in our search.

We need only locate a vertex u that points to t, then we can check to see if dist[u] + weight(u,t) is smaller than dist[t].

Much like Breadth First Search, we will start at a known source vertex, and set its distance to 0 while all other vertices get a computed distance of Infinity. We now place all of these vertices into a Priority Queue that records the shortest known distance to s for any vertex. In our core functioning loop, we retrieve a vertex that has the shortest distance computed from s and we expand from that direction only.

This is directly analagous to the Breadth First Search strategy, this time using the measure of "distance from s" as a means of ordering the vertices in a priority queue.

Once done, the following core loop will serve our purposes. We find a vertex that has shortest distance and remove it from the priority queue and see if we can reduce the computed shortest distances for all of its outgoing adjacent vertices.

while (!pq.isEmpty()) { int v = pq.delMin(); for (DirectedEdge e : G.adj(v)) { relax(e); } }

The definition of relax is as follows, and follows the earlier intuition:

void relax(DirectedEdge e) { int v = e.from(); int w = e.to(); if (distTo[w] > distTo[v] + e.weight()) { distTo[w] = distTo[v] + e.weight(); edgeTo[w] = e; pq.decreaseKey(w, distTo[w]); } }

Now, with this priority queue implementation, we use a special structure known as an IndexMinHeap which takes a basic heap structure and adds a specific capability, namely:

Determine existing index in heap for given key.
Allows you to decrease the priority for that key – essentially moving it closer to the front of the queue.
You can only decrease the priority key – you can never INCREASE the key. The issue can be seen in the implementation of decreaseKey in IndexMinHeap.

So now you have everything in place. Dijkstra’s algorithm methodically eliminates vertices from consideration one at a time (much like Breadth First Search does by marking vertices as they are encountered). In this case, however, they are "visited" in order of their shortest accumulated path from s. No longer do we mark vertices, but rather we maintain a priority queue of vertices that have yet to be visited. Once the priority queue is empty, we are done.

The details are found in the indexMinPQ class and are worth studying.

1.2 IndexMinPQ

IndexMinPQ is a Java class modified as follows from a standard Min priority queue. It is highly specialize for use with graph algorithms because it can only contain integer values that have an associated priority value (Key).

public class IndexMinPQ<Key extends Comparable<Key>> { int maxN; // maximum number of elements on PQ int N; // number of elements on PQ int[] pq; // binary heap using 1-based indexing int[] qp; // inverse of pq: qp[pq[i]] = pq[qp[i]] = i Key[] keys; // keys[i] = priority of i ... }

IndexMinPQ will never grow beyond its initial size, maxN+1.
N contains the number of integers currently contained in the min PQ.
pq stores the integer values in the priority queue.
qp describes *where* in the PQ a particular vertex exists.
keys contains the actual priority values (doubles).

This data type supports all priority queue operations with one addition, namely,

public void decreaseKey(int i, Key key) { keys[i] = key; swim(qp[i]); }

This powerful method is trivial to implement. Assuming that you know the given index, i, exists within the PQ, then this operation will reduce its value (wherever it happens to exist in the PQ) and cause it to "swim up" to maintain the heap property of the PQ.

1.3 Worked-out example on handout

You can show the structure of a graph from a text file

% java algs.days.day25.DigraphAdjacencyList day25.txt

To launch the example today, just run algs.days.day25.DijkstraSP which is pre-configured to execute this small example.

1.4 New example on IndexMinPQ

I have added a class, IndexMinPQExploration, that explains the inner workings of the IndexMinPQ.

1.5 Daily Question

The assigned daily question is DAY25

If you have any trouble accessing this question, please let me know immediately on Piazza.