CS 2223 Apr 01 2022

Lecture Path: 12
Back Next

Musical Selection: Peter Cetera: Glory of Love (1986)

Visual Selection: Sistine Chapel Ceiling, Michelangelo (1508-1512)

Live Selection:Spirit of Radio, Rush (2012)

Daily Question: DAY12 (Problem Set DAY12)

1 Heap Processing

To have faith is to trust yourself to the water. When you swim you don’t grab hold of the water, because if you do you will sink and drown. Instead you relax, and float.
Alan Watts

1.1 HW2

Opening discussion of HW2 here. Due Apr 04 2022 at 10AM.

Monday we will conduct a review to prepare for midterm. Homework3 will be assigned the day after Apr 05 2022 and will be due on Apr 19 2022.

1.2 Discussion of Modulo operator

In lecture on Thursday I was discussing the implications of using modulo operators as a costly operation. A student pointed out that the compiler should optimize modulor operators, but this is only possible if the constant is part of the code (rather than dynamically in a variable). Still, I thought to investigate.

1.3 Priority Queue Type

In the presentation on the Queue type, we discussed the nature of a queue as providing a "first in, first out" behavior. One naturally wonders whether it is possible to enqueue elements but then dequeue the element of "highest priority" still in the queue. This is the classic definition of a Priority Queue. To describe this as an API, consider the following operations that would be supported (p. 309):

There are other elements, but these are the starting point.

In our initial description, the Key values being inserted into the PQ are themsevles primitive values. In the regular scenario, the elements are real-world entities which have an associated priority attribute.

One solution is to maintain an array of elements sorted in reverse order by their priority. With each request to insert a key, place it into its proper sorted location in the array.

You could keep all elements in unsorted fashioin and then your delMax operation will take time proportional to the number of elements in the PQ.

No matter how you look at it, some of these operations take linear time, or time proportional to the number of elements in the array. Page 312 summarizes the situation nicely:

The alternate heap structure can perform both operations in log N time. This is a major improvement and worth investigating how it is done.

1.4 Heap Data Structure

We have already seen how the "brackets" for tournaments are a useful metaphor for finding the winner (i.e., the largest value) in a collection. It also provides inspiration for helping locate the second largest item in a more efficient way than searching through the array of size N-1 for the next largest item.

The key is finding ways to store a partial ordering among the elements in a binary decision tree. We have seen this structure already when proving the optimality of comparison-based sorting.

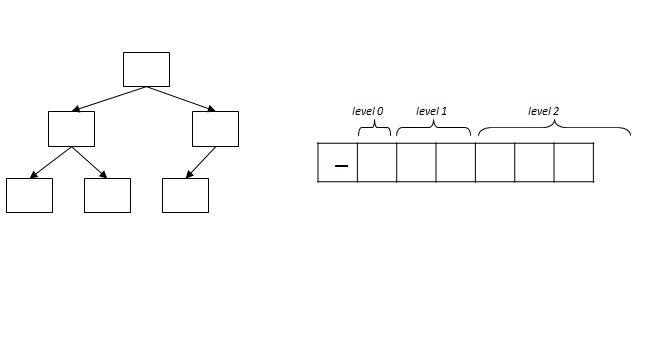
Consider having the following values {2, 3, 4, 8, 10, 16} and you want store them in a decision tree so you can immediately find the largest element.

Figure 1: Binary Decision Tree

1.5 Benefits of Heap

We have already seen how the concepts of "Brackets" revealed an efficient way to determine the top two largest elements from a collection in n + ceiling(log(n)) - 2 which is a great improvement over the naive 2n-3 approach. What we are going to do is show how the partial ordering of elements into a heap will yield interesting performance benefits that can be used for priority queues.

Definition: A binary tree is heap-ordered if the key in each node is larger than or equal to the keys in that node’s two children (if they exist).

But now we add one more property often called the heap shape property.

Definition: A binary tree has heap-shape if each level is filled "in order" from left to right and no value appears on a level until the previous level is full.

While the above example satisfies the heap-ordered property, it violates the heap-shape property because the final level has a gap where a key could have been placed.

Figure 2: Binary Heap

With this model in mind, there is a direct mapping of the values of a heap into an array. This can be visualized as follows:

Figure 3: Larger Heap Example

Each value at index k has potentially two children at indices 2*k and 2*k+1. Alternatively, each value at index k > 1 has its parent node at index floor(k/2).

There are two internal operations needed to maintain the structure of a heap.

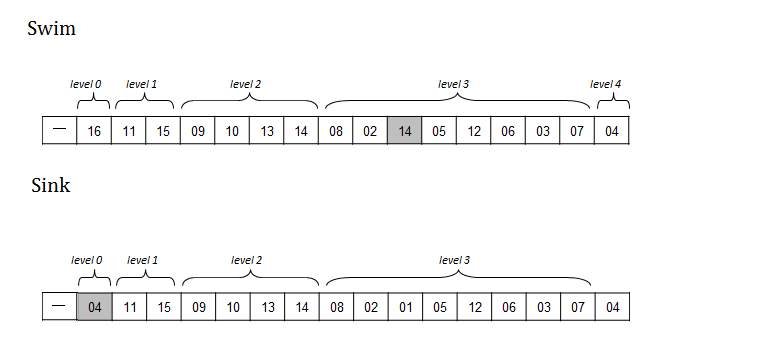
1.6 Swim – reheapify up

What if you have a heap and one of its values becomes larger than its parent. What do you do? No need to reorganize the ENTIRE array, you only need to worry about the ancestors. And since the heap structure is compactly represented, you know that (p. 314) the height of a binary heap is floor (log N). The height of a tree is the maximum depth among its nodes. A heap with just 1 element has a height of 0.

1.7 Sink – reheapify down

What if you have a heap and one of its values becomes smaller than either of its (potentially) two children? No need to reorganize the ENTIRE array, you only have to swap this value with the larger of its two children (if they exist). Note this might further trigger a sink, but no more than log N of them.

Figure 4: In class Example

1.8 Building a Heap

On page 318 of the book, you can see the disarmingly simple code for adding an element to a heap. In this case, we assume there is enough room in the array, but you should know how to add the necessary code to dynamically resize the array to add more space as needed.

public class MaxPQ<Key> { Key[] pq; // store items at indices 1 to N (pq[0] is unused) int N; // number of items on priority queue public MaxPQ(int initCapacity) { pq = (Key[]) new Object[initCapacity + 1]; N = 0; } public boolean isEmpty() { return N == 0; } public int size() { return N; } public void insert (Key v) { pq[++N] = v; swim(N); } }

This code first pre-increments N – recall that the 0th element of the array is not being used to make the indices easier to compute. Remember that a heap must maintain its Heap shape property, which means that you don’t add a new item to a level until the previous level is complete, and each level is filled from left to right in order. The pq[++N] = v statement does just that.

Once inserted, this new value might violate the Heap ordering property, so you have to invoke swim(N) to make sure that all ancestors are properly updated to abide by this property.

1.9 In-class exercise

Use this process to build a heap after the following values have been added in the following order:

2, 7, 4, 9, 8, 6

Assuming the array has enough room for the elements, what will be the final array representation in the resulting heap?

1.10 Removing an element from a Heap

Finding the largest element is not an issue becaue the topmost element in the heap a[1] is the largest value. However, once it is removed, what do we replace it with? I guess it could be replaced with the larger of its two children, but we have to be very careful to maintain the Heap Shape Property. Since adding to a heap was simply a matter of adding to the final unused element in the array, perhaps this remove operation could use that value as the replacement and then reduce the size of the heap by one.

public Key delMax() { Key max = pq[1]; exch(1, N−−); // swap final entry to replace root pq[N+1] = null; // to avoid loitering sink(1); // re-establish heap ordered property return max; }

Observe that the delMax operation reduces the number of elements in the array by one, and the Heap Shape Property is maintained by carefully mainpulating the elements. The sink(1) operation resetablishes the Heap Ordered Property and it takes no more than ~ log N operations to achieve this.

Given the final heap we just constructed, demonstrate the resulting array structure after invoking delMax two more times.

1.11 Big O Notation

The book covers Tilde notation in pages 180-187. As I’ve said in class, we are moving away from Tilde to a more formal notation used by Algorithm designers, and this will become increasingly important for the remaining homeworks.

There are two skills that you need to do:

Code Analysis: Given a block of code, analyze the order of growth (as a function of N) of the running time of the code fragment. Consider the following code. Think of the frequency of execution of the outer loop and the inner loops (see p. 181 for details).

int sum = 0; // Block A for (int n = N; n > 0; n /= 2) { // Block B for (int i = 0; i < n; i++) { // Block C sum++; } }

t1: A executes 1 time
t2: B executes ________ times
t3: C executes ________ times

Grand Total: ____________

The resulting Ordering Of Growth is going to be based on the formulae found on p. 187:

• 1 – constant

• log N – logarithmic

• N – linear

• N log N – linearithmic

• N2 – quadratic

• N3 – cubic

• bN – exponential (in any base b>1)

1.12 Daily Exercise

In an array, a repeater, is a value which appears more than n/2 times in an array of size n.

For this daily exercise, what if you had a heap of size n stored in an array and you were told that there is a repeater value in the heap. Can you guarantee that one of the leaf nodes is a repeater value? Either prove or provide a counter example.

1.13 Sample Exam Question

The following exam question is just a bit too hard to ask on the exam. But try it out and we will review in the next lecture:

You have an array of N elements in sorted order. You wish to use Binary Array Search to determine the rank for a target value, x. The only problem is, the compareTo(a, b) operator will lie exactly one time during your search. This function returns 0 if the values are the same, a negative number if a < b, and a positive number if a > b.

Complete the following skeleton algorithm (in pseudo code or Java code) and then identify the fewest number of less requests that your algorithm needs to accurately determine the rank of x.

(a) Design your algorithm in Java or pseudo code

int rank (Comparable[] a, Comparable x) { // fill in here... }

(b) Compute the fewest number of less requests needed in terms of N where N is the number of elements in the Comparable[] array.

1.14 Interview Challenge

Each Friday I will post a sample interview challenge. During most technical interviews, you will likely be asked to solve a logical problem so the company can see how you think on your feet, and how you defend your answer.

You have three pair of colored dice – one red, one green and one blue – and for each colored pair of dice, one of the die is lighter than the other. You are told that all of the light dice weigh the same. And also you are told that all of the heavy dice weigh the same.

You have an accurate pan balance scale on which you can place any number of dice. The scale can determine whether the weight of the dice on one side is equal to, greater, or less than the weight of the dice on the other side.

Task: You are asked to identify the three lightest dice from this collection of six dice.

Obvious Solution: You could simply conduct three weight experiments.

1. Put one red die on the left pan, and the other red die on the right pan – this will identify the lighter red die

2. Put one green die on the left pan, and the other green die on the right pan – this will identify the lighter green die

3. 3. Put one blue die on the left pan, and the other blue die on the right pan – this will identify the lighter blue die This takes three weighing operations.

Challenge: Can you locate the three lighter dice with just two weight experiments, where you can place any number of dice on either side of the pan.

1.15 Daily Question

The assigned daily question is DAY12 (Problem Set DAY12)

If you have any trouble accessing this question, please let me know immediately on Discord.

1.16 Version : 2022/04/02

(c) 2022, George T. Heineman