CS 2223 Mar 24 2022

Lecture Path: 07
Back Next

Musical Selection: Rick Springfield: Jessie’s Girl (1981)
Visual Selection: Primavera, Sandro Botticelli (1470s-1480s)
Live Selection:Take me to the pilot (1971), Elton John (1998)
Daily Question: DAY07 (Problem Set DAY07)

1 Mergers and Acquisitions

1.1 Homework due at 6PM today

At 10:30 PM Wednesday night, only 19 submissions for HW1.

At 6:30 AM Thursday morning, only 24 submissions.

I have had to move my 11AM office hours today up to 2PM. Hope you can still make it.

Note that Homework 2 is released today. Find it online. Code will be pushed tonight.

Selection Sort and Insertion Sort both operate in linear fashion. That is, they each seek to reduce the size of the problem by one with each iteration.

1.2 Preface Materials

Hmm, difficult. VERY difficult. Plenty of courage, I see. Not a bad mind, either. There’s talent, oh yes. And a thirst to prove yourself. But where to put you?
The Sorting Hat
Harry Potter and the Philospher’s Stone

But first, last year’s midterm has been posted in Canvas (see announcement to this effect). Note that you will see a question that asks for an extensive Tilde analysis of an algorithm. As I have said in class, I will no longer be focusing so intently on Tilde analysis, so that kind of question (Question #2) will not be on this year’s midterm exam.

1.3 Find Max Recursive

We will discuss this in class. Handout is available.

static int findMax(int[] A, int lo, int hi) { // Base Case: Only one element! if (lo == hi) { return A[lo]; } // Recursive Case: More than one element int mid = (lo+hi)/2; // Find L, max of left side, and R, max of right side int L = findMax(A, lo, mid); int R = findMax(A, mid+1, hi); // return larger of the two if (L > R) { return L; } else { return R; } }

1.4 Merge Sort

Can we find someway to divide the problem in half with each pass? MergeSort offers the ability to do just this.

Unfortunately, the first attempt at doing so typically leads to excessive wasted storage that slows everything down. Let’s show what the code would look like (find it in the repository as AnnotatedWastedSpaceMerge}.

public static void sort(Comparable[] a) { sort (a, 0, a.length-1); } static void sort (Comparable[] a, int lo, int hi) { if (hi <= lo) return; int mid = lo + (hi - lo)/2; sort(a, lo, mid); // recursively sort a[lo..mid] sort(a, mid+1, hi); // recursively sort a[mid+1..hi] merge(a, lo, mid, hi); // merge two together }

This is surprisingly succinct. To see the overall behavior, review AnnotatedWastedSpaceMerge} which shows the behavior when sorting an array of eight elements, a[0..7]:

sort(0,7) 1. sort(0,3) 1. 1. sort(0,1) 1. 1. 1. sort(0,0) 1. 1. 2. sort(1,1) 1. 1. 3. merge(0,1) 1. 2. sort(2,3) 1. 2. 1. sort(2,2) 1. 2. 2. sort(3,3) 1. 2. 3. merge(2,3) 1. 3. merge(0,3) 2. sort(4,7) 2. 1. sort(4,5) 2. 1. 1. sort(4,4) 2. 1. 2. sort(5,5) 2. 1. 3. merge(4,5) 2. 2. sort(6,7) 2. 2. 1. sort(6,6) 2. 2. 2. sort(7,7) 2. 2. 3. merge(6,7) 2. 3. merge(4,7) 3. merge(0,7)

The reason Mergesort works in the "real world" is that there is no need to worry about extra storage; as long as you have "room" on the table, then you will have place to put the merged results. But we don’t have that luxury in software. One option (which leads to wasteful space) is shown below.

To understand how the merge function works, recognize that it starts with a single array, a, that is sorted in ascending order from a[lo..mid]; in addition, a[mid+1..high] is also sorted in ascending order. This inefficient solution smakes a full copy of a[lo..hi] into aux (first for loop).

It then (in the second for loop) completes the merge. To see the "wasteful" memoray usage of this implementation, consider the output when sorting a number of sample arrays:

N Extra Estimate = 2*N*log N - 2*N 4 8 8.00 8 32 32.00 16 96 96.00 32 256 256.00 64 640 640.00 128 1536 1536.00 256 3584 3584.00 512 8192 8192.00

As you can see from the above table, if you allocate extra storage within merge, you quickly realize that you are simply wasting space. Fortunately, the fix is an easy one to make (p. 273). Instead of allocating the storage within each sort invocation, do so once when the function begins.

We are now ready to talk about the "in-place" merge sort.

So we need to explain how merge works with an auxiliary array, which is accessible to the merge function:

The key is the final for loop. While it looks complicated at first, you can break it down into four cases as follows, which matches the above code

• (left > mid) Have you exhausted left elements?

• (right > hi) Have you exhausted right elements?

• (less(aux[right]], aux[left]) Take element from right if smaller

• Else we take element from left because it is larger or equal

1.5 Recursive in-class demonstration

Work through example on small array (from p. 273)

E M R G E S O R

Review in debugger in Eclipse (AnnotatedMerge)

1.6 Comparison analysis

Mergesort uses between ~1/2 N log N and N log N comparisons to sort any array of length N (p. 272).

How can we show this? Let’s develop a mathematical model that counts the number of comparisons, C(n), for sorting n elements. For starters, let’s assume that n is a power of 2. This simplifies the accounting of operations, and in the long run, this won’t affect the results since we will be able to show that the result holds even for n that are not powers of two.

First focus on the number of comparisons in merge (a, lo, mid, hi). Consider when a[lo..mid] has two elements and so does a[mid+1..hi]. With each comparison you advance either i or j, and it is possible that this could happen just 3 times, before one of them fall off the range. Check this out yourself:

i: [ 2, 4 ] merge j: [ 1, 3]

is 1 < 2? Yes, so advance j
is 3 < 2? No, so advance i
is 3 < 4? Yes, so advance j

To generalize, you could go as far as N-1 comparisons where N is the sum of the lengths of the two arrays being merged.

In the best case, you would only compare N/2 elements since one would become exhausted.

So you can’t do FEWER than N/2 and you can’t do more than N-1.

To clean this up, we’ll just say:

So you can’t do FEWER than N/2 and you can’t do more than N.

So now ready for the big claim:

C(N) <= C(N/2) + C(N/2) + N
C(N) >= C(N/2) + C(N/2) + N/2

This is a very accurate evaluation. To compute the upper bound for C(N) we use the first equation above and try to find equality. That is, we start with the modeling equation:

C(N) = 2*C(N/2) + N

Now we assume N is a power of 2, or 2n. Thus we have

C(2n) = 2*C(2n-1) + 2n.

If you recursively replace the right-most C(2n-1) you get:

C(2n) = 2*[2*C(2n-2) + 2n-1] + 2n.

Let’s do one more time to see the effect:

C(2n) = 2*[2*[2*C(2n-3) + 2n-2] + 2n-1] + 2n.

If you expand out the multiplications, you get the following:

C(2n) = 8*C(2n-3) + 2n + 2n + 2n.

As you look at this equation, it looks like the following:

C(2n) = 2k*C(2n-k) + k*2n.

Now replace back:

C(N) = 2k*C(2n-k) + k*N

So the final question to ask is how large is k? The answer is log(N), at which point C(1) means no comparisons for a single element. Thus the final equation we develop is:

C(N) = 2n*C(1) + N * log (N)

But since C(1) is 0, this

C(N) = N * log N as an upper bound on the number of comparisons.

The analysis becomes more complicated when N is not a power of 2, but this suffices for lecture.

1.7 Array access analysis

Mergesort uses at most 6N log N array accesses. This works out in similar fashion and I won’t do it here (please see p. 275).

1.8 Comparison-based Sorting Proposition

So now let’s explain why the Merge Sort analysis interesting.

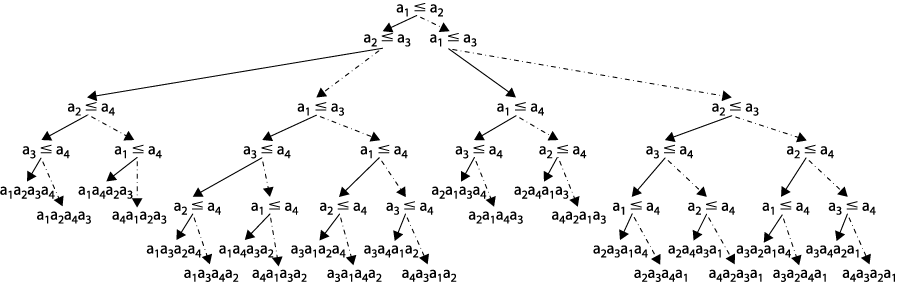
Remember the exercise to compute the fewest number of comparisons needed to sort five elements? If you use comparisons to sort elements, there are some fundamental limits that we can prove. First, consider the following decision tree that reflects the n! permutations of four elements:

Figure 1: Similar to p.281

First verify that all 4!=24 possible permutations exist as leaves in this decision tree. Now the question at hand is the maximum distance from the top decision (a1 <= a2) to any of the permutations.

There are some permutations that only require four comparisons (for example, the leftmost a1a2a3a4. But some require five comparisons, such as in the middle a4a3a1a2. Note that the maximum number of comparisons is 5.

Can we use this observation to make any claim about the maximum height of a decision tree for using comparisons to sort n elements? The answer is yes! First we need to state a properly of binary decisions trees, namely, that a tree with height h has no more than 2h leaves. And in fact, the tree of height h with the maximum number of leaves is perfectly balanced, or complete (see p. 281).

Second observe that the decision tree will have at least n! leaves; after all, you could have an algorithm that reaches the same sorted answer with a different ordering of comparison questions.

Thus N! <= number of leaves <= 2h

Take logarithm of both sides, and you see log(N!) <= h. So all you need is an approximation for log(N!). Try this:

log(N!) = log( N*(N-1)*(N-2)* ... *2*1 )
log(N!) > log( N*(N-1)*(N-2)* ... *N/2) Only go half way
log(N!) > log( (N/2)N/2) Simplify further
log(N!) > (N/2)*log(N/2)
log(N!) > (N/2)*(log N - 1)
log(N!) > (1/2)*N*log N - N/2

Now N*log N will grow more rapidly than N/2, so we can say (finally):

log(N!) is reasonably predicted by N log N

Because of this confirmation, you know that no sorting algorithm that uses comparisons can guarantee to use fewer than ~ N log N comparisons. This is a lower bound on the difficulty of the sorting problem.

No compare-based sorting algorithm can guarantee to sort N items with fewer than log(N!) comparisons. Note that log(N!) is ~ N log N.

This is a LOWER BOUND on the number of comparisons needed to sort elements.

Mergesort offers an UPPER BOUND on the number of comparisons that it uses.

With this in hand, we can assert the Mergesort is an asymptotically optimal compare-based sorting algorithm.

*whew*

1.9 Sorting a linked list

What if you were asked to sort a Linked list? values. I went ahead and did this, but note that this is different from maintaining an ordered list of values, I will show tomorrow.

Find the solution in LinkedListSort. I wondered whether Selection Sort or Insertion Sort would provide inspiration – it turns out that Selection Sort is more helpful. If the linked lists were doubly-linked (where each node also linked to its previous node) then it is likely that Insertion Sort would provide some guidance.

1.10 Daily Question

The assigned daily question is DAY07 (Problem Set DAY 07)

If you have any trouble accessing this question, please let me know immediately on Discord.

1.11 Version : 2022/03/28

(c) 2022, George T. Heineman