CS 2223 May 10 2021

Lecture Path: 26
Back Next

Expected reading: pp. 668-683
Daily Exercise:
Classical selection: Brahms Symphony No. 4 in E minor (1885)

Visual Selection:

Musical Selection: The Ballad of Loki: Songify the Avengers (2019)

Visual Selection: Libro de los juegos (1283)

Live Selection: Cantaloupe Island, Herbie Hancock, 1985

1 Advanced Search Techniques

1.1 Course Errata

Please continue to work on HW5.

If you do not change direction, you may end up where you are heading.
Lao Tzu

Also, please remember to complete the course evaluation survey, which is now available in Class Climate inside of Canvas. As of 9:00 AM Monday morning, 27 of you (23%) have completed the survey. This will be open for three additional days.

There will be two more daily questions (for a total of 24). Remember, that your grade is based on participation and you only need to complete 20 of these.

1.2 AStar Search Algorithm

We have seen a number of blind searches over graph structures. In their own way, each one stores the active state of the search to make decisions.

Breadth-First search – Expands the search by refusing to visit vertices n+1 edges away from the start until all vertices n have been searched.
Depth-First search – Expands the search by randomly choosing a direction, relying on backtracking (via recursion unwinding) to determine alternate routes
Dijkstra Single-source shortest-path – In searching for the shortest path, Dijkstra makes local decisions to expand the search in the shortest available direction.

These algorithms all make the following assumptions:

The graph exists in its entirety
We can identify the vertices in the graph using integers 0 to n-1
It is possible to mark which vertices have been visited
There is no way to "know" or "guess" the right direction to proceed

By relaxing these three assumptions we can introduce a different approach entirely that takes advantage of these fundamental mechanics of searching while adding a new twist.

In single-player solitaire games, a player starts from an initial state and makes a number of moves with the intention of reaching a known goal state. We can model this game as a graph, where each vertex represents a state of the game, and an edge exists between two vertices if you can make a move from one state to the other. In many solitaire games, moves are reversible and this would lead to modeling the game using undirected graphs. In some games (i.e., card solitaire), moves cannot be reversed and so these games would be modeled with directed graphs.

Consider the ever-present 8-puzzle in which 8 tiles are placed in a 3x3 grid with one empty space. A tile can be moved into the empty space if it neighbors that space either horizontally or vertically.

The following image demonstrate a sample exploration of the 8-puzzle game from an initial state.

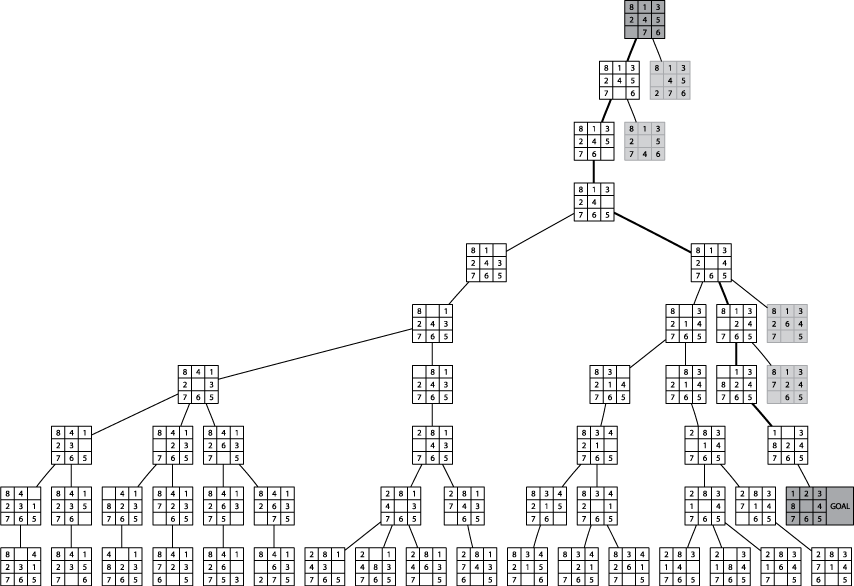
The goal is to achieve a clockwise ordering of tiles with 1 being placed in the upper left corner and the middle square of the grid being empty. Given this graph representation of a game state, how can we design a search algorithm to intelligently search from a starting point to the known goal destination state?

In the field of Artificial Intelligence (AI) this problem is known as Path Finding. The strategy is quite similar to the DFS and BFS searches that we have seen, but you can now take advantage of a special oracle to select the direction that the search will expand.

First start with some preliminary observations:

The graph is expanded as the search progresses and will never be fully realized.
Instead of marking vertices, maintain a closed collection of states that have already been visited. How can this be done efficiently?
Make intelligent choices during the search.

In the initial investigations into AI playing games from the 1950s, the following two types are strategies to use:

Type A: Consider every possible move and select best resulting state based on a scoring function.
Type B: Use adaptive decisions based upon the knowledge of the game to evaluate the "strength" of intermediate states.

While it is still difficult to develop accurate heuristic scoring functions, this is still an easier task than trying to understand game mechanics.

So we will pursue the development of a heuristic function. To explain how it can be used, consider the following template for a search function:

# states that are still worth exploring; states that are done. open = new collection closed = new collection add start to open while (open is not empty) { select a state n from open for each valid move at that state generate next state if closed contains next { // do something } if open contains next { // do something } else { add next state to open } }

In a Depth-First search of a graph, the open collection can be a stack, and the state removed from open is selected using pop.

The above image shows a max-Depth depth first search which stops searching after a fixed distance. Without this check, it is possible that a DFS will consume vast amounts of resources while darting here and there over a very large graph (on the order of millions of nodes).

In a Breadth-First search of a graph, the open collection is a queue, and the state removed from open is selected using dequeue.

The following represents a BFS on an eight-puzzle search:

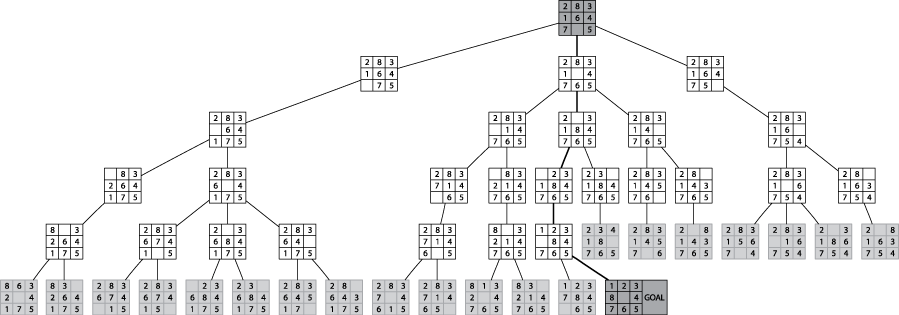
As you can see, this methodically investigates all board states K moves away before investigating states that are K+1 moves away.

Neither blind approach seems useful on real games.

Wouldn’t it be great to remove a state from open that is closest to the goal state? This can be done if we have a heuristic function that estimates the number of moves needed to reach the goal state.

1.3 Heuristic Function

The goal is to evaluate the state of a game and determine how many moves it is from the goal state. This is more of an art form than science, and this represents the real intelligence behind AI-playing games.

For example, in the 8-puzzle, how can you identify the number of moves from the goal state? You can review the Good Evaluator which makes its determination by counting the number of misplaced tiles while also taking into account the sequence of existing tiles in the board state.

The goal is to compute a number. The smaller the number is, the closer you are to the goal state. Ideally, this function should evaluate to zero when you are on the goal state.

With this in mind, we can now compute a proper evaluation function.

AStar search computes the following function for each board:

f(n) = g(n) + h(n)

Here g(n) is the current depth in the exploration from the start game state while h(n) represents the scoring heuristic function that represents the number of moves until the goal state is reached.

1.3.1 Comparing AStar to BFS

If the Heuristic function always returns 0, then AStar search devolves into BFS, since it will always choose to explore states that are K moves away before investigating states that are K+1 moves away.

It is imperative the the heuristic function doesn’t overestimate the distance to the goal state. If it does, then the AStar search will mistakenly select other states to explore as being more productive.

This concept is captured by the term admissible heuristic function. Such a function never overestimates, though it may underestimate. Naturally, the more accurate the heuristic function, the more productive the search will be.

1.3.2 Sample Behavior

The behavior of AStar is distinctive, as shown below:

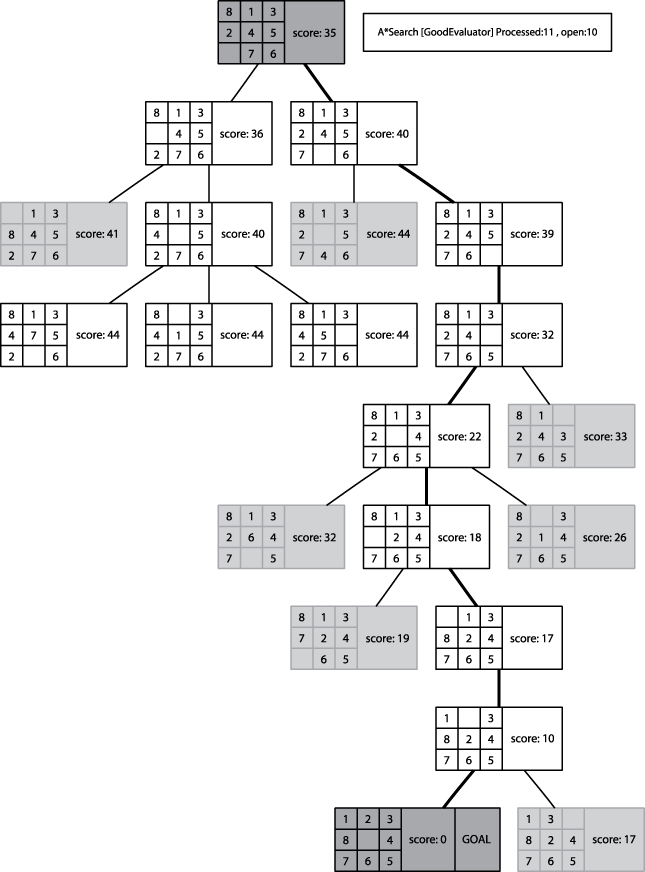
1.3.3 Modifying Open States

One thing that is common to both BFS and DFS is that vertices in the graph were marked and they were never considered again. We need a more flexible arrangement. Specifically, if we revisit a state which is currently within the open collection, though it hasn’t yet been selected, it may be the case that a different path (or sequence of moves) has reduced the overall score of g(n) + h(n). For this reason, AStar Search is represented completely using the following algorithm:

public Solution search(EightPuzzleNode initial, EightPuzzleNode goal) { OpenStates open = new OpenStates(); EightPuzzleNode copy = initial.copy(); scoringFunction.score(copy); open.insert(copy); // states we have already visited. SeparateChainingHashST<EightPuzzleNode, EightPuzzleNode> closed; while (!open.isEmpty()) { // Remove node with smallest evaluated score EightPuzzleNode best = open.getMinimum(); // Return if goal state reached. if (best.equals(goal)) { return new Solution (initial, best, true); } closed.put(best,best); // Compute successor states and evaluate for (SlideMove move : best.validMoves()) { EightPuzzleNode successor = best.copy(); move.execute(successor); if (closed.contains(successor)) { continue; } scoringFunction.score(successor); EightPuzzleNode exist = open.contains(successor); if (exist == null || successor.score() < exist.score()) { // remove old one, if it exists, and insert better one if (exist != null) { open.remove(exist); } open.insert(successor); } } } // No solution. return new Solution (initial, goal, false); }

To understand why this code can be efficient, focus on the key operations:

retrieve state with lowest score in open collection
add state to closed
determine if closed contains state
check if open contains state
remove state from open
insert state into open

Clearly we want to use a hash structure to be able to quickly determine if a collection contains an item. This works for the closed state, but not for the open state.

Can you see why?

So we use the following hybrid structure for OpenStates:

public class OpenStates { /** Store all nodes for quick contains check. */ SeparateChainingHashST<EightPuzzleNode, EightPuzzleNode> hash; /** Each node stores a collection of INodes that evaluate to same score. */ AVL<Integer,LinkedList> tree; /** Construct hash to store INode objects. */ public OpenStates () { hash = new SeparateChainingHashST<EightPuzzleNode, EightPuzzleNode>(); tree = new AVL<Integer,LinkedList>(); } }

1.3.4 Demonstration

8 puzzle demonstrations: 8puzzle animations (DFS,BFS,AStarSearch)

Note that it has been shown that every 8-puzzle board state can be solved in 31 moves or less.

So why not just do a depth first search and set a max depth of 31? Can you estimate the size of the search tree? It comes down to fan-out, which is based on the number of available moves in any given state (which is based on the location of the empty square). On average, fan-out is the average of {2, 3, 2, 3, 4, 3, 2, 3, 2} = 24/9 = 2.666, so 2.6631 ~=~ 1.6 x 1013.

Do you find it suprising that with a standard 3x3 rubik’s cube, it has been proved that you can solve any valid random rubik’s cube in 20 moves or less (where any movement of a face counts as a move)? If you prefer the more rigorous quarter-turn metric (where you count each 90-degree rotation of a face as being a move) then the number is 26.

1.3.5 So how good is A* Search

Well, if you try it on larger problems, such as the 15-puzzle, you will find that the search space is too large for most scrambled initial states.

computation

Enter the above into GraphViz Online

And you will produce the following image:

Clearly there are opportunities to improving the evaluation of a 15-puzzle board state. If you want to tackle this on your own, visit Algorithms in a nutshell (2ed).

1.4 Efficient algorithm for 15-puzzle?

Often an algorithm tailored for a specific domain will outperform any general-purpose search algorithm. Ian Parberry (1997) developed an efficient O(N3) algorithm for solving any N2-1 puzzle (such as the 8-puzzle or the 15-puzzle).

procedure puzzle(n) { if n == 3 then solve brute force else use greedy algorithm to complete first row and column puzzle(n-1) }

Find details about this algorithm in this paper.

1.5 Daily Question

If you have any trouble accessing this question, please let me know immediately on Discord.