CS 2223 Apr 20 2021

Lecture Path: 16
Back Next

Expected reading: pp. 406-411 (Order-based Methods & Deletion)

Classical selection: Dvorak: Symphony No. 9 "New World" (1893)

Visual Selection:

Musical Selection: Vanilla Ice: Ice Ice Baby (1990)

Visual Selection: Solitary Tree, Caspar David Friedrich (1822)

Live Selection:Garfunkel / Bridge over Troubled Water (Central Park, 1981)

1 Working With BSTs

1.1 Grading Updates

All daily questions are properly scored in canvas (remember: this is participation grade). Average is an 84%. Please take advantage of these daily questions to improve your overall grade, and perhaps change a B into an A.

Midterm grades are now done: compare this year’s result to prior years.

2021: 81.7
2019: 72.15
2018: 74.1

Biggest change? Average on Q2 went from 10 points to 15 points.

Currently we have 43% of the points in the books.

1.2 Quality of echo360 live stream

I will run a simultaneous Zoom meeting (using my office hours link) at 10:00 AM to try to see if zoom can share the screen with increased quality.

Find the zoom link in Canvas.

1.3 Big Picture

There are three things that I want everyone to get from this class:

An understanding of the fundamental data types available in computer science. This includes a description of the performance expectations of the key methods from the interface and how you can implement these types using specific data structures to meet these performance targets. I believe you have to implement a data structure to truly understand it.
An introduction to Asymptotic Analysis of algorithms. This is the big O notation I have introduced in the past two weeks. I can only give a cursory introduction to this subject, but hopefully point you in the right direction if you are interested in learning more about the mathematical modeling behind algorithms.
Fundamental families of algorithms necessary to function as a computer scientist or data scientist. At the highest level, this means to learn about overall approaches for searching, symbol tables, sorting, and other niche algorithms that are appropriate and will be discussed in due time.

1.4 BST Lecture

We will cover the fundamental data structure in computer science, called the Binary Search Tree (BST). This extremely versatile data structure gives us the dynamic behavior that you have seen with linked list while retaining the ~ log N search time we have seen for ordered binary array search.

In short, if you understand binary search trees, you know 50% of all the data structures used by computer science. It is that important.

We are going to stay here for awhile. It is important that you understand BSTs and can work with them on a practical and theoretical level.

1.5 Structure

The fundamental structure of a BST is a node in the tree. This node contains a (key, value) pair because the BST implements the Symbol Table API that we have already seen.

class Node { Key key; Value val; Node left, right; // left and right subtrees int N; // number of nodes in subtree (incl. self) public Node(Key key, Value val, int N) { this.key = key; this.val = val; this.N = N; } }

While it seems similar to a linear linked list, observe that there are two pointers from each node. With this extra information, we will be able to construct trees of information. We use the term tree because at no point will you be able to find a loop, much like how each linked list was guaranteed to terminate.

Here is a sample Binary Search Tree (BST):

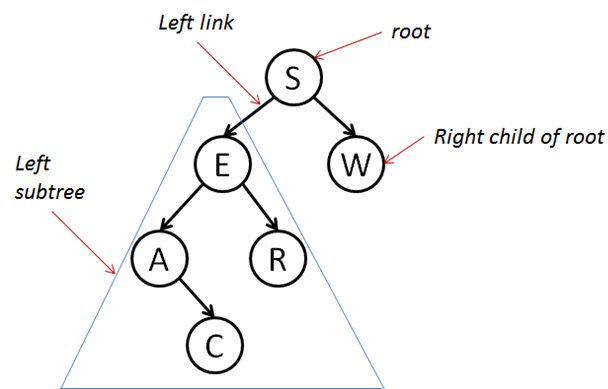
The term tree may look odd, but this is how we draw trees in computer science. We start with the root at the top, and then grow downwards. Structurally, each node has up to two children.

The intuition behind BST is that we can structure values in specific ways to achieve impressive efficiencies.

Some definitions are important:

A link is either a reference to the left or right child of a node. We also use (interchangeably) the term edge.
The height of a node is the number of edges from that node to its most distant leaf. What follows is that the height of any leaf node is zero.
The height of a tree is the height of its root.
The depth of a node is the number of edges from the root to that node. What follows is that the depth of the root is zero.

Can you work out this definition?

Note that the height property for a node can be recursively defined in terms of the two children of a node.

1.6 Binary Search Tree property

The fundamental idea behind BST is that each node has potentially two subtrees, a left subtree and a right subtree. Given any node N in the BST, you are guaranteed that:

Each of the keys in the left subtree n.left are guaranteed to be smaller than or equal to n.key.
Each of the keys in the right subtree n.right are guaranteed to be larger than or equal to n.key.

1.7 Constructing a BST

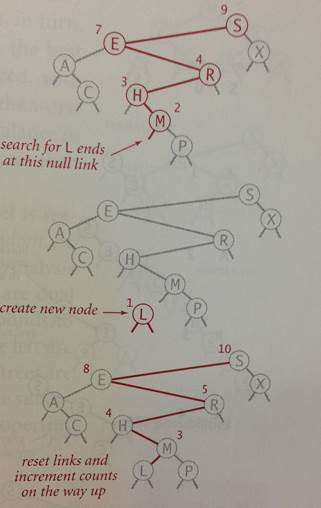
You construct a BST by adding (key,value) pairs to it, one at a time. If the root of a tree is empty when you add the first node, then it must be created and it becomes the root of the tree. So in the above example, you should be able to guess that "S" was the first value entered into the tree.

Repeat this outloud so you really understand this helper method. By defining in this way, we avoid lots of annoying special cases.

The code for put requires some contemplation. There is a helper method put(parent, key, value) which adds a node representing (key,value) to belong to the tree rooted at parent.

If parent is null, then we create a new BST and return that as the BST.

Note that this means the helper put method returns a BST in all cases. In particular, this also means that if we were to add "E" as the second letter in the above BST, then parent would be the root. Since "E" is smaller than "S" we want to add this value to the left subtree. However, there is no left-subtree (yet) so it is created by the following code.

public void put(Key key, Value val) { root = put(root, key, val); } // Adds a node for (key, val) to belong to tree rooted // at parent and return root of that tree. Node put(Node parent, Key key, Value val) { if (parent == null) return new Node(key, val, 1); int cmp = key.compareTo(parent.key); if (cmp < 0) parent.left = put(parent.left, key, val); else if (cmp > 0) parent.right = put(parent.right, key, val); else parent.val = val; parent.N = 1 + size(parent.left) + size(parent.right); return parent; }

We will spend time going over some examples.

1.8 Searching for value in BST

Searching is straightforward from the structure. We look for a value by starting at a parent node. If we have found it in that node, it is returned, otherwise we investigate either the left or the right branch, depending upon the relationship between the target key and the node’s key.

public Value get(Key key) { return get(root, key); } Value get(Node parent, Key key) { if (parent == null) return null; int cmp = key.compareTo(parent.key); if (cmp < 0) return get(parent.left, key); else if (cmp > 0) return get(parent.right, key); else return parent.val; }

1.9 Recursion and Put

Page 401 of the Sedgewick book contains a nice graphic explaining how the put method works. More importantly, the accompanying text does a fine job in explaining the nature of the recursive calls that you see within the BST implementation.

Well, I’m ramblin’, ramblin’ ’round, I’m a ramblin’ guy, I’m ramblin’, oh, yes, oh, yes! I’m a ramblin’ guy - R-A-M-B-L-I-N apostrophe, oh yes, I’m ramblin’
Steve Martin

----

In this example, you are adding the letter to an existing BST. Starting at the root, you recursively move down until you get to a node that is larger than you AND has no left child. Once inserted, the function recursively walks backward in response to these functions returning. Each time up the value of N is updated to reflect the proper count.

If you do not understand the recursive nature of this computation, please come to office hours.

1.10 Computing Min and Max in a BST

BSTs are an extremely versatile data structure and supports a wide range of potential functionality. We compare each of these operations using three structures already covered:

-	min/max	get	floor/ceiling	int rank	select nth	put
SortedArray	1	~log N	~log N	~log N	1	N
BST	~log N	~log N	~log N	~log N	~log N	~log N
ChainST	~N	~N/M	~N	*	*	1

Note that the BST in all cases can guarantee "~log N" behavior with reasonable distribution of the keys in the BST. Thus the reason these operations can all be performed in ~log N is because the height of a balanced binary tree is guaranteed to be logarithmic with respect to the number of keys, N, in the tree. This proposition only holds if the tree is guaranteed to be balanced and we will address that topic on Day 18 (Apr 23 2021).

1.11 Min discussion

To find the minimum key in a BST, simply start at the root node and keep following the left child until there are no more left children. That node is the minimum key in the BST.

public Key min() { return min(root).key; } private Node min (Node parent) { if (parent.left == null) { return parent; } return min(parent.left); }

This is one of the simplest methods to implement. On handout, let’s review execution performance for analysis.

Many of the recursive examples shown in this chapter can be replaced with non-recursive counterparts, but there is no immediate guarantee that this will lead to noticeably faster code.

Consider eliminating recursion from the min method as shown on the handout. This works on this simple example, but not for Floor.

1.12 Computing Floor(key) in BST

Let’s tackle a more challenging question. How about returning the keys in a BST that are closest to a target key, without actually being present in the BST? We use the mathematical concept of Floor and Ceiling as follows:

Floor – find the largest key that is smaller than target
Ceiling – find the smallest key that is larger than target

In a way, you have seen this concept in Binary Array Search. Try the following example by hand:

Search for the value 7 in a sorted array:

+—+—+—+—+—+—+—+—+—+—+—+—+ | 2 | 3 | 5 | 9 | 10| 11| +—+—+—+—+—+—+—+—+—+—+—+—+ 0 1 2 3 4 5 (0) lo mid hi (1) lo mid hi (2) lo mid hi (3) hi lo

When Binary Array Search complets without finding a value, note that the value of lo points to the entry which is the smallest value larger than the target (which makes that the ceiling of 7. To locate the floor, simply look at A[lo-1] to find that element.

Note that the above formulation must be carefully handled when looking for the ceiling of a target greater than any element in the array, or for the floor of a target smaller than any element in the array.

Given this definition of Floor, let’s review the code.

public Key floor(Key key) { Node rc = floor(root, key); if (rc == null) return null; return rc.key; } private Node floor(Node parent, Key key) { if (parent == null) return null; int cmp = key.compareTo(parent.key); if (cmp == 0) return parent; // Found: this is floor if (cmp < 0) return floor(parent.left, key); // key smaller? try left Node t = floor(parent.right, key); // greater? parent might if (t != null) return t; // be floor, but only if return parent; // no other candidate }

1.13 Delete Min or Delete Max

Precursor to describing the real delete method which will be focus of tomorrow’s lecture. Start by recognizing that it is simple to remove a node from a tree that only has a single child (whether left or right).

It is straightforward to locate the minimum key in the tree (as we have already seen) so now we want to remove its Node from the tree

public void deleteMin() { if (root != null) { root = deleteMin(root); } } Node deleteMin(Node parent) { if (parent.left == null) { // delete occurs here return parent.right; } parent.left = deleteMin(parent.left); parent.N = size(parent.left) + size(parent.right) + 1; return parent; }

This code must make sure that it enforces the BST property as well as updating the associated N attribute with the ancestor nodes that are affected by the deletion.

1.14 Pre-Order Traversing a Tree

The most important thing about a Binary Search Tree is that all of the keys are maintained in order. And more importantly, they can be retrieved in order with a careful strategy.

Let’s start by coming up with a way of visiting every key in a BST. We will call this a PreOrder traversal. Start at the root node and do the following:

Circle node if you haven’t already visited it. Output its key
Pre-order visit left subtree, if it exists
Pre-order visit right subtree, if it exists

// invoke a pre-order traversal of the tree public void preorder() { preorder(root); } void preorder(Node n) { if (n == null) { return; } StdOut.println (n.key); preorder (n.left); preorder (n.right); }

Try this on a sample tree and see what you get as output.

1.15 In-Order Traversing a Tree

While pre-order is interesting, a more relevant traversal is in-order traversal:

In-order visit left subtree, if it exists
Circle node if you haven’t already visited it. Output its key
In-order visit right subtree, if it exists

// invoke a in-order traversal of the tree public void inorder() { inorder(root); } void inorder(Node n) { if (n == null) { return; } inorder (n.left); StdOut.println (n.key); inorder (n.right); }

Try this on a sample tree and see what you get as output.

1.16 Asymptotic Analysis

You can find a wealth of information on Algorithms on the Internet. This Khan Academy Algorithms presentation is of higher quality:

In particular, you can start with