CS 2223 Apr 26 2018

Lecture Path: 25
Back Next

Expected reading: pp. 638-657
Daily Exercise:
Classical selection: Beethoven: Piano Sonata No. 14 "Moonlight" (1802)
Musical Selection: Len: Steal My Sunshine (1999)

There should be no such thing as boring mathematics
Edsger Dijsktra

1 Single-Source Shortest Path

We now have an algorithm for computing the single-source, shortest path within a weighted, directed graph containing non-negative weights. With the code shown yesterday, the performance is classified as O((V+E) * log V). The book (proposition R on page 654) shortens this to O(E log V) in the worst case. This can be done because E is the dominant value when compared with V.

What if you instead implement the Digraph using an AdjacencyMatrix. What changes with regards to the code, and possibly, the overall performance.

1.1 AdjacencyMatrix representation

An Adjacency matrix representation creates a two-dimensional array which stores the potential edge weights.

public class DigraphAdjacencyMatrix extends EdgeWeightedDigraph{ double[][] weights; public DigraphAdjacencyMatrix (int V) { super(V); weights = new double[V][V]; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { weights[i][j] = Double.NEGATIVE_INFINITY; } } } ... }

We have some choices for specifying "no-edge". One idea is to use an edge weight of "0" for that purpose. Still, we might find ourselves with a graph in which we might allow edge-weights of 0, so we choose to declare a non-existent edge with Double.NEGATIVE_INFINITY.

This representation is unable to determine all adjacent vertices without checking through all possible candidates, thus:

public Iterable<DirectedEdge> adj(int v) { Queue<DirectedEdge> queue = new Queue<DirectedEdge>(); for (int i = 0; i < V; i++) { if (weights[v][i] != Double.NEGATIVE_INFINITY) { queue.enqueue(getEdge(v,i)); } } return queue; }

The reason this becomes a problem for the algorithms we are discussing is that we have been making a common assumption regarding performance of the following code:

for (int u = 0; u < g.V(); u++) { for (int v : g.adj(u)) { statement } }

Earlier this week, I argued that the above code executes statement E times for directed graphs and 2E times for undirected graphs.

Now, however, with an adjacency matrix, the above code will require time that is directly proportional to V2, since the outer u loop executes V times, and each pass through g.adj(u) requires V times as well.

Even worse, the above code is wasteful in that it constructs a queue to contain all edges, when in fact you would do better to optimize the DijkstraSP code to work directly off of a 2D array.

N E list-time matrix-time 128 2488 0.000000 0.000000 256 9999 0.000000 0.000000 512 39555 0.000000 0.000000 1024 157364 0.000000 0.016000 2048 628841 0.000000 0.047000 4096 2515264 0.015000 0.156000

Using the small example code (CompareDensePerformance), the performance is 10x slower with matrix representation.

1.2 Variations on Single-Source Shortest Path

There are several variations that might be considered (p. 654).

1.2.1 Undirected graphs

1.2.2 Directed Acyclic Graphs

What if you know the graph is a DAG, that is, there are no cycles? A more efficient variation of Dijkstra’s SP algorithm (page 658) is to relax the vertices in topological sort order. Since you know there are no cycles, each edge is going to be visited exactly once. This approach doesn’t need to use a priority queue, which means its performance is based on the performance of Topological Sort (p. 583) which means the worst case is O(E + V). This is a noticeable improvement over O(E*log V).

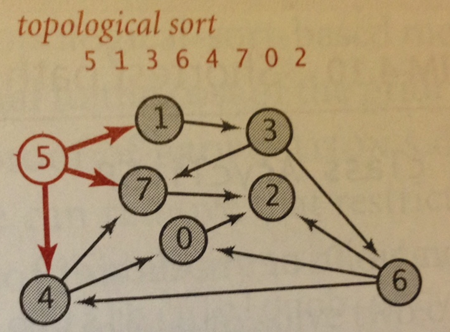
Here is a sketch of the algorithm. Once the topological order is computed, you process each vertex in order, relaxing all edges from those vertices. Note there is no need to use a priority queue because you rely on the topological sort to give you the vertices in a proper order; certainly, you might find a better shortest path with more edges, which forces a relax operation, but this won’t affect the order in which you process the vertices

// Relax without a priority queue since Acyclic void relax (EdgeWeightedGraph G, int v) { for (DirectedEdge e : G.adj(v) { int w = e.to(); if (dist[w] > dist[v] + e.weight()) { distTo[w] = dist[v] + e.weight(); edgeTo[w] = e; } } } void shortestPath(EdgeWeightedGraph G, int s) { Topological top = new Topological(G); // Process each vertex in order for (int v : top.order()) { relax (G,v); } }

1.2.3 Negative Edge Weights

What if we wanted to allow edge weights to be negative. This fundamentally alters the nature of the problem.

Note that Dijkstra’s SP algorithm used a priority queue to determine the order of vertices to investigate. And the claim was that the vertices removed from the priority queue were done in shortest distance from the source. This claim was made possible because successive paths only increased the total distance, so now our original assumption is invalid.

Consider the following small graph:

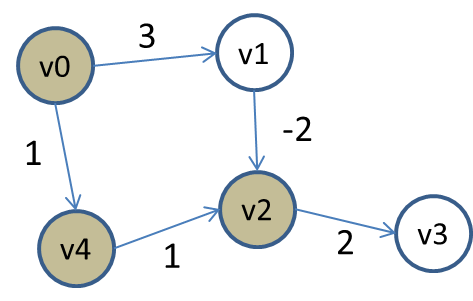
The vertices are colored based on whether they have been processed and removed from the priority queue. As usual, we compute Single-Source Shortest path starting from vertex v0. After inserting vertices v1 and v4 into the priority queue, the algorithm removes vertex v4 because its distance (1) is shorter than to v1 (3). Then vertex v2 is inserted into the priority queue. At this point, the priority queue contains two vertices with the following distance (aka, priorities):

• v1 with distance 3

• v2 with distance 2

Naturally, it removes v2 from the priority queue and eventually v3 is added with a total distance/priority of 4.

As you can see, Dijsktra’s SP algorithm just "assumes" that any edge coming from v1 to v2 will only increase the total accumulated weight, and so it chooses incorrectly, ultimately determining that the shortest distance to v3 is 4.

There is one more awkward situation to deal with. What if there is a negative cycle, that is, a directed cycle whose total weight (sum of the weights of the edges) is negative. If such a cycle existed, one could arbitrarily lower the total path cost by simply iterating through thus cycle as many times as you would like. So we must find a way to detect negative cycles in any graph that allows negative weights.

1.3 Bellman-Ford Algorithm

The book describes Bellman-Ford in a way that is more complicated than it needs to be. Bellman-Ford has the same approach that Dijkstra’s has, namely, find some edge to relax (or lower) distance. However, instead of trying to find vertices of which we relax individual edges, Bellman-Ford processes all edges within a fixed number of iterations.

for (int i = 1; i <= n; i++) { // for each edge in the graph, see if we can relax for (DirectedEdge e : G.edges()) { if (relax(e)) { if (i == n) { return; // negative cycle. DONE } } } }

And here is the relaxation code, as expected. For convenience, it returns true if the edge reduces the best shortest path.

boolean relax(DirectedEdge e) { int v = e.from(); int w = e.to(); if (distTo[w] > distTo[v] + e.weight()) { distTo[w] = distTo[v] + e.weight(); edgeTo[w] = e; return true; } return false; }

The best part of Bellman-Ford is that you don’t need to check for negative cycles. In each iteration (there are N of them) you process all edges to see if you can relax the distance. If you make a full pass over all the edges and you did not find a single edge to relax, then you know that you are done.

Let’s analyze the performance of this code. The outer for loop executes V time, and the inner for loop executes E times, thus the performance of this code is Θ(E*V).

However, what if you keep making iterations, and keep finding edges that seem to relax a distance, here and there. How do you know if you are still making progress to the actual solution? It turns out there is a very simple answer to this question.

I’ll start by asking this: What is the longest possible path between any two vertices in a directed weighted graph? Well, if there are V vertices, then it must be V-1 edges.

So, thinking along the lines of breadth first search, if you start at a source and complete one iteration over all edges, you know that you have the shortest distance between source and all vertices one edge away. After the second iteration, you know that you have the shortest distance between source all all vertices two (or fewer) edges away. If you continue through V-1 iterations, you will have completed the solution.

However, what if a negative cycle exists? Well, then go ahead and iterate one more time, and if you find an edge that relaxes a distance value, you know there must be a negative cycle.

This is why the for loop iterates exactly V times.

There is also a nice optimization here. It may turn out that after a few iterations, you find no other edge that can be relaxed. In this case, perhaps long before V, you can stop and declare a solution.

If you look at the code, you will see how we handle these two edge cases.

1.4 Sample Exam Questions

1.4.1 Recurrence Relation

We are using big O notation to classify algorithms according to how their running time or space requirements grow as the input size grows.

Let T(n) represents the time/performance of an algorithm on an input of size n.

(1) Develop a recurrence relation for T(n) for the following code; and then (2) classify the worst case performance of the algorithm using Ω(f(n)), Θ(f(n)), and O(f(n)):

public int compute (int N, int k) { if (k <= 1) { return 0; } int count = 0; for (int j = 0; j < Math.sqrt(N); j++) { count++; } return count + compute (N, k/2); }

1.4.2 Binary Search Tree

You are given a standard BST in which each node stores a value N, that reflects the total count of nodes in the subtree rooted at the node. Note that a leaf node has N=1.

Write a recursive method that returns the kth smallest value in the tree, for k in [0, size) where size is the number of values in the BST. You can assume you have a method size(Node n) that returns the size of the sub-tree rooted at n, or 0 if n is null.

Fill in as follows:

public Key select(int k) { ... } public Key select (Node parent, int k) { ... }

1.4.3 Big Theta Notation

Can you explain why "T(n) = N - 999" is classified as Θ(N).

Try to find c1 such that for all N > n0, c1*N < N - 999.

Now try to find c2 such that for all N > n0, c2*N > N - 999.

If you can find these three constants (c1, c2 and n0) then you can claim that T(n) is Θ(N).

1.5 Version : 2018/04/22

(c) 2018, George Heineman