CS 2223 Apr 12 2018

Lecture Path: 19
Back Next

Expected reading: 515-527
Daily Exercise:
Classical selection: Beethoven Symphony No. 2 (1802)
Musical Selection: UB40: Can’t Help Falling In Love (1993)

Yoda: No more training do you require. Already know you, that which you need.
Luke: Then I am a Jedi.
Yoda: No. Not yet. One thing remains. Vader. You must confront Vader. Then, only then, a Jedi will you be. And confront him you will.
Star Wars: Episode VI

1 Graphs and Next Steps

1.1 Homework 3 questions

In the rubric for question 3 on the homework, you can see 5 points for "code for computing Cn". Cn is defined as the internal path length of a tree which is computed as the sum of the depth of each node in the tree.

There are two ways to write such a method.

Store depth – As each node is inserted into the BST you would store its depth. This alternative is more complicated for a variety of reasons.
Compute depth – As you traverse the nodes in a binary search tree, you do so in a very specific order, starting with the root which is at depth 0, then moving on to its left and right children, which are at depth 1, and so on...

Note that this computation requires a bit of time to think and work through, which is why it wouldn’t appear on an exam, but it is a good question to have on a homework assignment.

1.2 Graphs

We are now studying a new domain in computer science called Graphs. A graph represents not just a set of items but the relationships between those items, which may be dynamically changed.

Figure 1:

Figure 2:

It is truly interesting to study graphs because there are several possible structures you can use to implement graphs, and there is no standardized solution that everyone agrees with.

Figure 3:

Start with some definitions:

A graph is a set of vertices and a collection of edges that each connect a pair of vertices.

Note that the graph is defined by a set of vertices; each vertex is therefore unique. Each vertex may have any number of edges (zero or more). However, it is common to avoid the following situations:

Self-loops: when a vertex has edge back to itself
parallel edges: when a vertex has multiple edges to the same paired vertex.

For our purposes, we will focus on simple graphs that avoid these two anomalies.

In this first lecture we are going to cover a number of new terms that are necessary to understand within the domain of graphs.

Vertex u is adjacent to vertex v if there exists an edge (u,v) in the graph.
A subgraph is a subset of a graph’s edges and the vertices that are connected to those edges.
A path is a sequence of vertices connected by edges.
A cycle is a path with at lease one edge whose first and last vertices are the same.
The length of a path or a cycle is the number of edges in the path.
A graph is connected if there is a path from every vertex to every other vertex in the graph.

1.3 Trees

We have covered the Binary Tree structure in the context of Binary Search Trees, but when we come to graphs, the term Tree is a more generalized term.

A Tree is a graph that is fully connected and contains no cycles.

1.4 Code Example

The bulk of this lecture is to understand the code handout. This implementation is just one of three possible ways to structure the data for a graph.

1.5 Structural Concerns

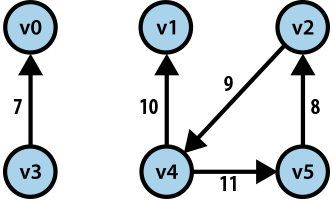
The vertices in a graph are essentially abstract concepts. For convenience, then, we simply refer to each vertex by 0, 1, ..., V-1 for a graph with V vertices.

For the algorithms we cover, we do not address situations where a vertex is added or removed; adding this capability doesn’t really change the complexity of the algorithms.

Naturally it becomes more convenient to have "names" or other arbitrary data associated with each vertex. To make this work, we will use the following standard:

SeparateChainingHashST<String,Integer> map = new SeparateChainingHashST<>(); SeparateChainingHashST<Integer,String> reverse = new SeparateChainingHashST<>();

map takes an arbitrary string and returns its associated vertex number (0, 1, ..., V-1) while reverse takes a given vertex number and returns its associated string. With these structures, we can retrieve (in ~ constant time) the necessary information for a vertex.

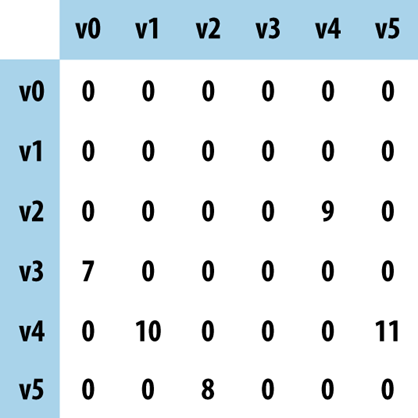
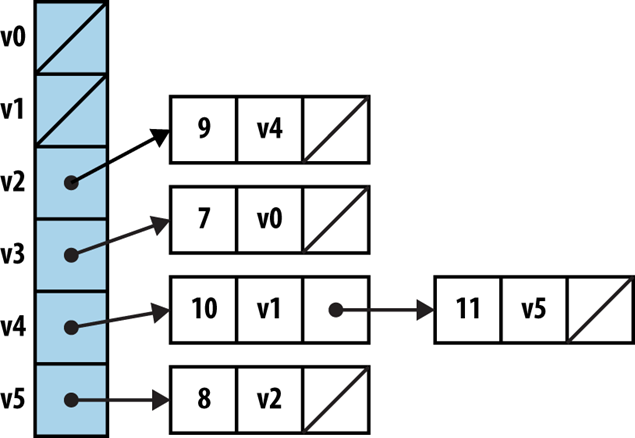
We can store a graph using any of the data structures we have seen so far. Two possibilities immediately come to mind:

Figure 4:

Figure 5:

Which of these solutions is "best"? Well, it depends on the nature of the information you are storing

In 2012, Airports Council International (ACI) reported a total of 1,598 airports worldwide in 159 countries, resulting in a two-dimensional matrix with 2,553,604 entries. How many of these entries has a value? Well, that depends on the number of direct flights. ACI reported 79 million "aircraft movements" in 2012, roughly translating to a daily average of 215,887 flights. Even if all of these flights represented an actual direct flight between two unique airports (clearly the number of direct flights will be much smaller), this means the matrix is 92% empty. This is a good example of a sparse graph.

A complete graph is one where there is an edge between a vertex and every other vertex in the graph.

Since there could be on the order of V*(V+1)/2 possible edges in a graph with V vertices, then in a dense graph, the number of edges is proportional to the square of the number of vertices. In a sparse graph, the number of edges is proportional to the number of vertices.

1.6 Mathematical Analysis

When analyzing graphs and graph algorithms, we will typically use two variables in our formulae:

V – The number of Vertices
E – The number of Edges

And often the performance of a specific algorithm will improve (or degrade) based on whether a graph is sparse or dense.

1.7 Tomorrow’s lecture

Note that I was not able to secure a meaningful guest lecturer for tomorrow, so instead I will be recording my lecture tonight and posting it online.

I wish I could have been giving this lecture in real-time, so I could answer your questions. Please write down the questions that you do have, and post them to Piazza and I will address them when I get the chance. I am traveling all weekend but I should have some time to address them.

Note that I will not have online office hours on Sunday April 15th, but I will have online office hours tonight.