CS 2223 Apr 09 2018
Expected reading: pp. 412-413
Daily Exercise: Count Leaves
Classical selection:
Haydn Trumpet Concerto in E Flat (1796)
Musical Selection:
Jesus Jones: Right Here, Right Now (1991)
Out, damn’d spot! out, I say! – One; two: why, then ’tis time to do’t –
Hell is murky
Lady Macbeth
1 Iterators and Deletion
1.1 Homework 3
Rubric for HW3 is now posted. I’ve added some more explanation to the HW3 description to show the expected format for the output.
1.2 First a small puzzle
Have you ever been asked one of these MatchStick puzzles? Given the following image, move just one matchstick to create five squares of equal size:
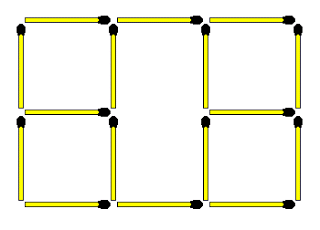
Discussion ensues.
1.3 Deleting Arbitrary Elements in BST
The goal is to delete a key from a BST with the least amount of effort. Doing so is like the matchstick problem.
Now we face the challenging issue of deleting elements anywhere in the BST.
Just to set the stage, construct BST after adding following values in this order:
M, S, A, L, T, O
With this BST in hand, propose a new BST that could result if you were to delete the key M:
Discussion ensues.
1.3.1 Hibbard Deletion technique
The deletion of a Node with two children requires special handling. Fortunately, with the intuition from above, we can see how this might be implemented. Knowing what is supposed to happen is just as important as understanding how this compact code works.
public void delete(Key key) { root = delete(root, key); } private Node delete(Node parent, Key key) { if (parent == null) return null; // recurse until you find node with this key. int cmp = key.compareTo(parent.key); if (cmp < 0) parent.left = delete(parent.left, key); else if (cmp > 0) parent.right = delete(parent.right, key); else { // handle easy cases first: if (parent.right == null) return parent.left; if (parent.left == null) return parent.right; // has two children: Plan on returning min of our right child Node old = parent; parent = min(old.right); // Will eventually be "new parent" // Note this is a simpler case: Delete min from right subtree // and DON’T FORGET to stitch back in the original left child parent.right = deleteMin(old.right); parent.left = old.left; } // as recursions unwind, update size appropriately parent.N = size(parent.left) + size(parent.right) + 1; return parent; }
The key to understanding deletion is breaking the problem into smaller subproblems; in this case, reducing it to the simpler deleteMin case we already covered.
If you never recursively locate a node with the sought for value, then you will eventually bottom out the recursion. Note that as the recursions unwind, the size will be updated, even though nothing was deleted.
However, should a node with the desired key be identified, the two easy cases where that node has a single child are handled immediately. But if there are two children, we know that we want to replace parent node with the smallest node in its right subtree. We thus locate this minimum and then in just a few statements we only need to move a single node to reestablish the Binary Search Tree property. Note that the unwinding of the recursion properly ensures that the N attribute is set correctly.
1.4 InOrder Traversal
What if you wanted to demonstrate a traversal that visited all keys in the BST in order? This is the reason that BSTs are so powerful. Let’s make a small change to the traversal algorithm:
public void inorder() { inorder(root); StdOut.println(); } private void inorder(Node n) { if (n == null) { return; } inorder (n.left); StdOut.print (n.key + " "); inorder (n.right); }
The order of the statements is critical! Revisit the earlier BST and try an inorder traversal.
Note that the (revised) code for today has pre-order and in-order traversals as well.
1.5 New Type: Ordered Symbol Table
You may recall from my earlier discussion of Symbol Tables that they give up any right to maintain ordering information about its elements.
On page 366 of Sedgewick, a new type is defined, Ordered Symbol Table, which aims to give one the flexibility of a symbol table while retaining all of the benefits of maintaining ordering information.
Now the class definition is: class ST<Key extends Comparable<Key>, Value> which means that there is a (Key, Value) pair stored in the ST for each Key, but now two keys can be compared to see which is lesser than, equal to, or greater than each other.
Operation | Description |
put (Key key, Value value) | Associate (key,value) in table |
Value get (Key key) | retrieve value for key |
void delete (Key key) | remove (key,value) pair in table |
boolean contains (Key key) | check if table has key |
int size() | return number of pairs |
boolean isEmpty() | determine if empty |
---- | ---------------------------- |
Key min() | return smallest key |
Key max() | return largest key |
Key floor(Key key) | return largest key <= key |
Key ceiling(Key key) | return smallest key >= key |
int rank(Key key) | return number of keys less than key |
Key select(int k) | return key of rank k |
void deleteMin() | delete smallest key |
void deleteMax() | delete largest key |
---- | ---------------------------- |
Iterable<Key> keys() | all keys in sorted order |
Iterable<Key> keys(Key lo, Key hi) | keys in [lo..hi] in sorted order |
1.6 Iterators
Prior to the midterm, I stayed away from describing the different Iterators as outlined in the book since I wanted to reduce the amount of material you needed to know for the midterm. Now that milestone is past, we have to cover Iterators.
Iterable Collections were first introduced on p. 123 and was presented as a means of processing each of the items in a collection. Using Iterators, one can write clear and compact code that frees the client from having to know about the underlying representation of the data types that it uses. This is an important software engineering issue and it appears here under the guise of designing APIs properly.
In Java, you know that an Iterator is being used when the enhanced for loop is written. This concept would appear in code as follows:
Bag<Double> numbers = new Bag<Double>(); numbers.add(17); numbers.add(13); numbers.add(19); for (Double d : numbers) { StdOut.println(d); }
1.6.1 Stack Iterator
The first Iterator presented is the Stack Iterator, which outputs the values in the stack in reverse order, with the clear intention of explaining to the client the order in which the values would be popped.
On Day4 (Mar 16 2018) I presented the ResizingArrayStack example which contained an iterator, but I didn’t present it in class. Here is the basic structure that you need to know:
package algs.days.day04; public class ResizingArrayStack<Item> implements Iterable<Item> { /** Iterates over contents in reverse LIFO order. */ public Iterator<Item> iterator() { return new ReverseArrayIterator(); } private class ReverseArrayIterator implements Iterator<Item> { private int i; // current position in stack public ReverseArrayIterator() { i = N-1; } public boolean hasNext() { return i >= 0; } public void remove() { } public Item next() { return a[i−−]; } } }
For the record, my implementation is slightly different than what you see in the book, while being functionally equivalent.
Key points are:
Stack implements Iterable interface – this declares to everyone that it has a method iterator() which will generate on demand an Iterator object to visit every element in stack.
ReverseArrayIterator is an internal class to ResizingArrayStack so it has access to its class attribute, N.
ReverseArrayIterator has internal attribute i which keeps track of the current index of the iterator, decrementing until it goes negative, which signals that it is done.
Demonstrate on working code (IteratorExploration).
1.6.2 Bag Iterator
Bag iterator works with linked list, rather than array, and the iterator is similarly straightforward.
private class ListIterator implements Iterator<Item> { private Node current; public ListIterator(Node first) { current = first; } public boolean hasNext() { return current != null; } public void remove() { } public Item next() { Item item = current.item; current = current.next; return item; } }
Note how the iterator once again maintains the state of the iteration, this time with a Node current attribute to point to the individual node in the linked list. The ListIterator is an inner class to Bag so it can access the Node class.
Demonstrate by running the modified Bag class which you find in the GitHub repository for today.
1.6.3 MaxPQ
There is no Iterator defined for the MaxPQ as implemented using a Heap structure. In a way, this makes sense, since one would like to get the elements in the same order that they would be retrieved; however to do this properly, you would have to destructively modify the heap – something you didn’t have to do with either the Stack or Bag iterator.
1.6.4 Symbol Table
The Symbol Table description (p. 366) uses a slightly different API for iteration, and this was based on the difference between a straight Symbol Table (which I introduced last week) and an Ordered Symbol table (which I omitted from discussion before the midterm).
Specifically, a client typically needs to get all keys for a Symbol Table. For Homework3, I made this available as part of the SequentialSearchST class. However, since the Symbol table was not ordered, the keys were returned much like the iterator for a Bag.
So now, I ask you... can we use an Iterator for a Binary Search Tree which will return the keys in sorted order? This is the killer application, if you will, for BSTs. So here are the two interfaces for Symbol Tables (p. 366):
Iterable<Key> keys () // all keys Iterable<Key> keys (Key lo, Key hi) // just keys in [lo..hi]
Naturally, the second method only works if the <Key> generic class is itself Comparable, but that is something you know is true for Binary Search Trees.
But now it is not clear how to implement this interface. The following methods do the trick, and they are patterned after the traversal steps we saw earlier. The solution is to use a Queue to accumulate the keys that are visited during the recursive invocations, and then it is a simple matter for a client to process the values from a Queue in order to retrieve the original keys.
public Iterable<Key> keys() { return keys(min(), max()); } public Iterable<Key> keys(Key lo, Key hi) { Queue<Key> queue = new Queue<Key>(); keys(root, queue, lo, hi); return queue; } private void keys(Node node, Queue<Key> queue, Key lo, Key hi) { if (node == null) return; // check if contained within this range int cmplo = lo.compareTo(node.key); int cmphi = hi.compareTo(node.key); // much like a traversal; builds up state in the queue. if (cmplo < 0) keys(node.left, queue, lo, hi); if (cmplo <= 0 && cmphi >= 0) queue.enqueue(x.key); if (cmphi > 0) keys(node.right, queue, lo, hi); }
Note that the keys method might make two recursive calls. But this is not something to worry about. Why? Because for every Iterator that returns N items, there is typically no way to avoid having ~N performance.
Here, assuming that the tree is balanced, we can see that the number of comparisons made during keys is no worse than:
C(N) = 2 + C(N/2) + C(N/2)
C(N) = 2*C(N/2) + 2
This happens in a balanced BST because the number of children "should be" evenly split between left and right children. Let’s telescope this term a few times:
C(N) = 2*[2*(C(N/4) + 2)] + 2
C(N) = 4*C(N/4) + 4 + 2
C(N) = 4*[2*C(N/8) + 2] + 4 + 2
C(N) = 8*C(N/8) + 8 + 4 + 2
Note that the sum of the additive terms are going to be smaller than 2*8 (more specifically, it will be exactly equal to 2*8 - 2)
If we continue this trend – and we assume – that N is a power of 2, then we have:
C(2n) = 2n*C(N/2n) + 2N-2
Eventually, C(1) is equal to zero, so we will compute the number of comparisons for keys to be ~2N in the worst case.
1.7 Daily Exercise
Complete the following code, which computes the number of leaf nodes in a tree.
/** Returns number of leaf nodes in the tree. */ public int countLeaves() { ... } /** Returns number of leaf nodes in the sub-tree rooted at parent. */ public int countLeaves(Node parent) { ... }
1.8 Version : 2018/04/11
(c) 2018, George Heineman