CS 2223 Apr 05 2018

Lecture Path: 15
Back Next

Expected reading: 396-405
Daily Exercise:
Classical selection: Tchaikovsky: Romeo & Juliet, Overture-Fantasy (1880)
Musical Selection: Tears for Fears: Sowing the Seeds of Love (1989)

Two roads diverged in a yellow wood,
And sorry I could not travel both
And be one traveler, long I stood
And looked down one as far as I could
To where it bent in the undergrowth;
Robert Frost

1 Binary Search Trees

1.1 Exam1 returned today

Exam1 will be returned today. Here are the statistics:

avg 73.76 14.90 13.13 15.83 15.39 14.50 stdev 15.65 4.48 4.45 4.42 4.18 3.93 74% 66% 79% 77% 73% LAST OFFERING: avg 73.96 13.52 12.98 17.28 15.39 14.79 stdev 13.79 4.74 4.96 3.11 4.32 4.01 68% 65% 86% 77% 74%

(#30) 86 or higher – Doing Very Well. Think "A" grade. Keep it up!
(#50) 72 to 84 – Good Job. Think "B" grade
(#27) 56 to 70 – Needs Improvement. Think "C" grade
(#19) below 56 – At risk. Be sure to review progress and talk to me

1.2 Homework 3

Homework 3 is being released today. It will cover some of the material from the last week as well as provide a starting point for Binary Search Trees.

1.3 Big Picture

There are three things that I want everyone to get from this class:

An understanding of the fundamental data types available in computer science. This includes a description of the performance expectations of the key methods from the interface and how you can implement these types using specific data structures to meet these performance targets. I believe you have to implement a data structure to truly understand it.
An introduction to Asymptotic Analysis of algorithms. I can only give a cursory introduction to this subject, but hopefully point you in the right direction if you are interested in learning more about the mathematical modeling behind algorithms.
Fundamental families of algorithms necessary to function as a computer scientist or data scientist. At the highest level, this means to learn about overall approaches for searching, symbol tables, sorting, and other niche algorithms that are appropriate and will be discussed in due time.

1.4 BST Lecture

We will cover the fundamental data structure in computer science, called the Binary Search Tree (BST). This extremely versatile data structure gives us the dynamic behavior that you have seen with linked list while retaining the ~ log N search time we have seen for ordered binary array search.

In short, if you understand binary search trees, you know 50% of all the data structures used by computer science. It is that important.

We are going to stay here for awhile. It is important that you understand BSTs and can work with them on a practical and theoretical level.

1.5 Structure

The fundamental structure of a BST is a node in the tree. This node contains a (key, value) pair because the BST implements the Symbol Table API that we have already seen.

class Node { Key key; Value val; Node left, right; // left and right subtrees int N; // number of nodes in subtree public Node(Key key, Value val, int N) { this.key = key; this.val = val; this.N = N; } }

While it seems similar to a linear linked list, observe that there are two pointers from each node. With this extra information, we will be able to construct trees of information. We use the term tree because at no point will you be able to find a loop, much like how each linked list was guaranteed to terminate.

Here is a sample Binary Search Tree (BST):

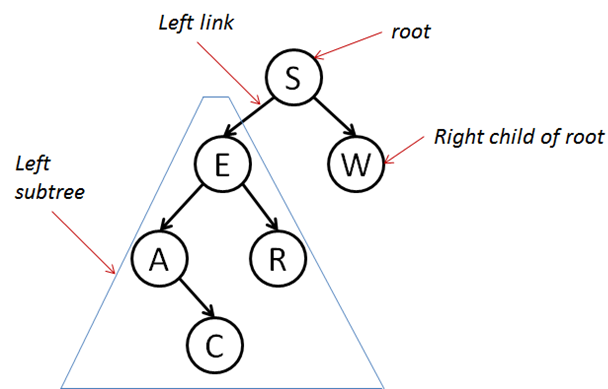
The term tree may look odd, but this is how we draw trees in computer science. We start with the root at the top, and then grow downwards. Structurally, each node has up to two children.

The intuition behind BST is that we can structure values in specific ways to achieve impressive efficiencies.

Some definitions are important:

A link is either a reference to the left or right child of a node. We also use (interchangeably) the term edge.
The height of a node is the number of edges from that node to its most distant leaf. What follows is that the height of any leaf node is zero.
The height of a tree is the height of its root.
The depth of a node is the number of edges from the root to that node. What follows is that the depth of the root is zero.

Can you work out this definition?

Note that the height property for a node can be recursively defined in terms of the two children of a node.

1.6 Binary Search Tree property

The fundamental idea behind BST is that each node has potentially two subtrees, a left subtree and a right subtree. Given any node N in the BST, you are guaranteed that:

Each of the keys in the left subtree n.left are guaranteed to be smaller than or equal to n.key.
Each of the keys in the right subtree n.right are guaranteed to be larger than or equal to n.key.

1.7 Constructing a BST

You construct a BST by adding (key,value) pairs to it, one at a time. If the root of a tree is empty when you add the first node, then it must be created and it becomes the root of the tree. So in the above example, you should be able to guess that "S" was the first value entered into the tree.

Repeat this outloud so you really understand this helper method. By defining in this way, we avoid lots of annoying special cases.

The code for put requires some contemplation. There is a helper method put(parent, key, value) which adds a node representing (key,value) to belong to the tree rooted at parent.

If parent is null, then we create a new BST and return that as the BST.

Note that this means the helper put method returns a BST in all cases. In particular, this also means that if we were to add "E" as the second letter in the above BST, then parent would be the root. Since "E" is smaller than "S" we want to add this value to the left subtree. However, there is no left-subtree (yet) so it is created by the following code.

public void put(Key key, Value val) { root = put(root, key, val); } Node put(Node parent, Key key, Value val) { if (parent == null) return new Node(key, val, 1); int cmp = key.compareTo(parent.key); if (cmp < 0) parent.left = put(parent.left, key, val); else if (cmp > 0) parent.right = put(parent.right, key, val); else parent.val = val; parent.N = 1 + size(parent.left) + size(parent.right); return parent; }

We will spend time going over some examples.

1.8 Searching for value in BST

Searching is straightforward from the structure. We look for a value by starting at a parent node. If we have found it in that node, it is returned, otherwise we investigate either the left or the right branch, depending upon the relationship between the target key and the node’s key.

public Value get(Key key) { return get(root, key); } Value get(Node parent, Key key) { if (parent == null) return null; int cmp = key.compareTo(parent.key); if (cmp < 0) return get(parent.left, key); else if (cmp > 0) return get(parent.right, key); else return parent.val; }

1.9 Final BST thoughts

Get prepared to read the text and to work on lots of small examples. You need very up-close and personal experience with BSTs and that is going to be the focus for the next week.

1.10 Dominant Example

I added better documentation to the Dominant Example from Day13, and I encourage you to review it. Execute the code to see how well the actual performance compares with the predicted behavior.