CS 2223 Mar 26 2018

Lecture Path: 09
Back Next

Expected reading: 308-314
Daily Exercise:
Classical selection: Beethoven: Sonata No 21 ’Waldstein’ (1804)
Musical Selection: Billy Joel: Tell Her About It (1983)

Another general shout!
I do believe that these applauses
are for some new honours
that are heap’d on Caesar.
Julius Caesar
William Shakespeare

1 Priority Queues

1.1 Sorting Summary

We could have spent several weeks on sorting algorithms, but we still have miles to go before we sleep, so let’s quickly summarize. We covered the following:

• Insertion Sort

• Selection Sort

• Merge Sort

• Quick Sort

For each of these, you need to be able to explain the fundamental structure of the algorithm. Some work by dividing problems into subproblems that aim to be half the size of the original problem. Some work by greedily solving a specific subtask that reduces the size of the problem by one.

For each algorithm we worked out specific strategies for counting key operations (such as exchanges and comparisons) and developed formulas to count these operations in the worst case.

We showed how the problem of comparison-based sorting was asymptotically bounded by ~N log N comparisons, which means that no comparison-based sorting algorithm can beat this limit, though different implementations will still be able to differentiate their behavior through programming optimizations and shortcuts.

1.2 Yesterday’s Daily Exercise

How did people fare on evaluating the recursive solution in terms of the maximum number of comparisons?

You should have been able to declare C(n) as the number of comparisons and then defined its behavior as:

C(N) = C(N/2) + C(N/2) + 1

assuming that N=2n as a power of 2.

C(N) = 2*C(N/2) + 1
C(N) = 2*(2*C(N/4) + 1) + 1
C(N) = 2*(2*(2*C(N/8) + 1) + 1) + 1

and this leads to...

C(N) = 8*C(N/8) + 4 + 2 + 1

since N = 2n and we are still at k=3...

C(2n) = 2k*C(N/2k) + (2k-1)

Now we can continue until k = n = log N, which would lead to...

C(2n) = 2n*C(N/2n) + (2n-1)

and since C(1) = 0, we have

C(N) = N - 1

1.3 Homework1

The leaderboard for TwiceSorted_Solution is as follows:

Participant	Num Inspections
Heineman	1460
Kyle Ehrlich	1533
Ben Slattery	1538
Connor Anderson	1862
James Kenney	1915
Nicholas Krichevsky	2097
Sathwik Karnik	2124
Pavee Phongsopa	2266
Ben Anderson	2318
Niall Dalton	2318
Yuxiang Mao	2378

Figure 1: Overall Results

Last year’s average for HW1 was 87.5. This year, the average is 91.5; I’m glad to see the results are improved from last year. Now let’s see how these results translate into HW2, which is harder and there is less time to complete.

1.4 Homework2

If I come up with anything to talk about regarding HW2, that goes here...

For the sorting comparisons, you should make a local copy of Quick within your USERID.hw2 package so you can use it directly within your SortComparison.

Be sure to replace "USERID" with your CCC credentials. For example, my email address is "heineman@wpi.edu" so my USERID would be "heineman".

For empirical analysis of the MultiSet implementation, use the ValidateMultiSet class which I have checked into the Git repository. Simply pull the latest from Git and copy this file into your hw2 package.

Finally: Regarding QuickSort, note that Shuffle is called prior to calling sort internally. Since you want to do an accurate accounting of all less and exch invocations, you will need to modify your code appropriate to include these counts as well.

1.5 Priority Queue Type

In the presentation on the Queue type, there was some discussion about a type of queue in which you could enqueue elements but then dequeue the element of "highest priority." This is the classic definition of a Priority Queue. To describe this as an API, consider the following operations that would be supported (p. 309):

Operation	Description
MaxPQ(n)	create priority queue with initial size
insert	insert key into PQ
delMax	return and remove largest key from PQ
size	return # elements in PQ
isEmpty	is the priority queue empty

There are other elements, but these are the starting point.

In our initial description, the Key values being inserted into the PQ are themsevles primitive values. In the regular scenario, the elements are real-world entities which have an associated priority attribute.

One solution is to maintain an array of elements sorted in reverse order by their priority. With each request to insert a key, place it into its proper sorted location in the array.

Now, you can use binary array search to find where the key can be insertedm but then you might have to move/adjust N elements to insert the new item into its position.

But doesn’t this seem like a lot of extra work to maintain a fully sorted array when you only need to retrieve the maximum value?

You could keep all elements in unsorted fashioin and then your delMax operation will take time proportional to the number of elements in the PQ.

No matter how you look at it, some of these operations take linear time, or time proportional to the number of elements in the array. Page 312 summarizes the situation nicely:

Data Structure	insert	remove max
sorted array	N	1
unsorted array	1	N
impossible	1	1
heap	log N	log N

The alternate heap structure can perform both operations in log N time. This is a major improvement and worth investigating how it is done.

1.6 Heap Data Structure

We have already seen how the "brackets" for tournaments are a useful metaphor for finding the winner (i.e., the largest value) in a collection. It also provides inspiration for helping locate the second largest item in a more efficient way than searching through the array of size N-1 for the next largest item.

The key is finding ways to store a partial ordering among the elements in a binary decision tree. We have seen this structure already when proving the optimality of comparison-based sorting.

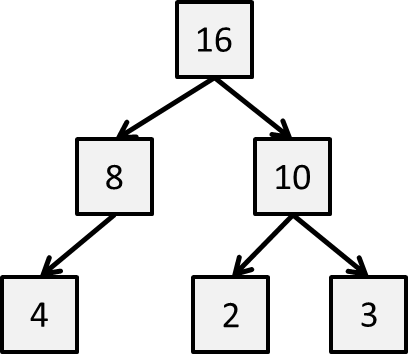
Consider having the following values {2, 3, 4, 8, 10, 16} and you want store them in a decision tree so you can immediately find the largest element.

Figure 2: Binary Decision Tree

1.7 Benefits of Heap

We have already seen how the concepts of "Brackets" revealed an efficient way to determine the top two largest elements from a collection in n + ceiling(log(n)) - 2 which is a great improvement over the naive 2n-3 approach. What we are going to do is show how the partial ordering of elements into a heap will yield interesting performance benefits that can be used for both priority queues (today’s lecture) and sorting (Thursday’s lecture)

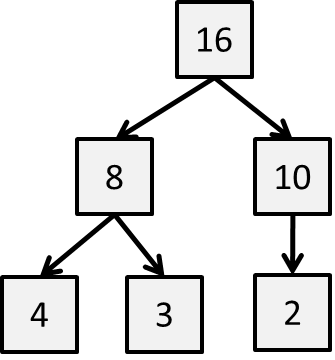
Definition: A binary tree is heap-ordered if the key in each node is larger than or equal to the keys in that node’s two children (if they exist).

But now we add one more property often called the heap shape property.

Definition: A binary tree has heap-shape if each level is filled "in order" from left to right and no value appears on a level until the previous level is full.

While the above example satisfies the heap-ordered property, it violates the heap-shape property because the final level has a gap where a key could have been placed.

Figure 3: Binary Heap

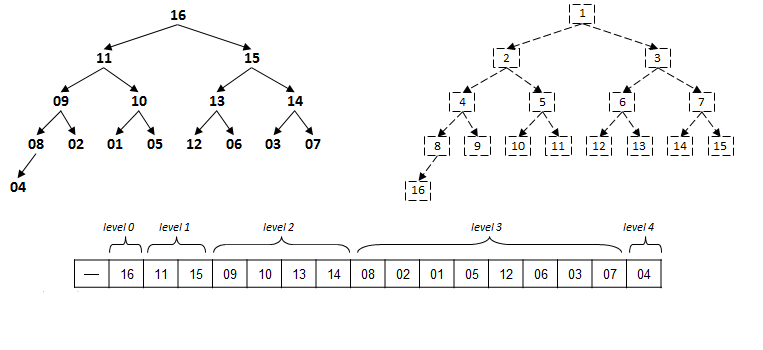
With this model in mind, there is a direct mapping of the values of a heap into an array. This can be visualized as follows:

Figure 4: Larger Heap Example

Each value at index k has potentially two children at indices 2*k and 2*k+1. Alternatively, each value at index k > 1 has its parent node at index floor(k/2).

1.8 Heap Problem for HW2

You are to get some experience with the MaxPQ type, which you can find in the Git repository under today’s lecture.

There are two internal operations needed to maintain the structure of a heap. For now we focus on the mechanisms and you will see their ultimate use on the homework assignment and the lecture on Mar 27 2018.

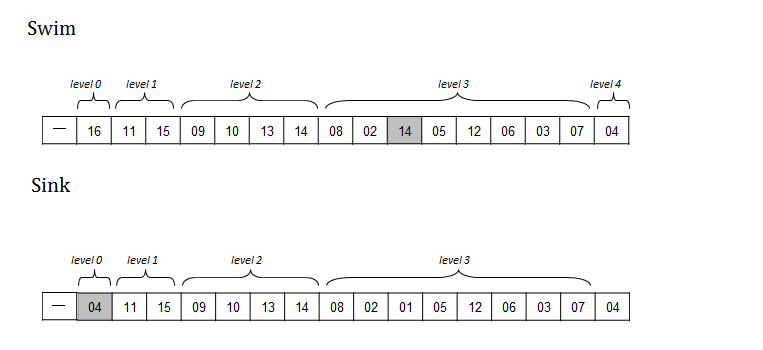
1.9 Swim – reheapify up

What if you have a heap and one of its values becomes larger than its parent. What do you do? No need to reorganize the ENTIRE array, you only need to worry about the ancestors. And since the heap structure is compactly represented, you know that (p. 314) the height of a binary heap is floor (log N).

1.10 Sink – reheapify down

What if you have a heap and one of its values becomes smaller than either of its (potentially) two children? No need to reorganize the ENTIRE array, you only have to swap this value with the larger of its two children (if they exist). Note this might further trigger a sink, but no more than log N of them.

Figure 5: In class Example

1.11 Version : 2018/03/27

(c) 2018, George Heineman