CS 2223 Mar 15 2018

Lecture Path: 03
Back Next

Expected reading: pp. 96-99, 121-129
Assume you know: pp. 64-89
Daily Exercise: Sorting Five Values
Classical selection: Grieg Piano Concerto in A major (1868)
Musical Selection: Cold as Ice, Foreigner (1977)

Wirth’s Law: Software is getting slower more rapidly than hardware becomes faster.
Nicholas Wirth

1 Well Begun Is Half Done

1.1 Important concepts from readings

Today I asked you to read about three fundamental data types in computer science. These are Bag, Stack and Queue. Two of these (Stack and Queue) are already implemented by the JDK (as class java.util.Stack and interface java.util.Queue). You need to understand the interfaces for all three data types. You need to understand the choices you make when implementing them.

1.2 Opening Questions

First let’s complete the accurate accounting to find the greatest and second greatest elements in a collection of N elements. Given just a small sample, you can see the following:

Size	Number Operations
2	1
3	3
4	4
7	8
8	9

Let’s start with the question I asked you to consider last lecture:

• What is the fewest number of comparisons to sort five elements?

Here is my solution. Discuss.

This question is of interest theoretically because we still don’t know the fewest number of comparisons to sort sixteen elements. Latest research from 2011 confirms that 46 comparisons suffices and that 44 do not. You would make international news if you could prove that 45 comparisons sufficed. Find the table of best comparison results on Wikipedia.

1.3 Data Types

The famous computer scientist Nicklaus Wirth published an influential book called "Algorithms + Data Structures = Programs (1978)." You need to understand these fundamental data types so you will be ready to tackle the more advanced ones later in this course.

Operation	Bag	Queue	Stack
add	add(Item)	enqueue(Item)	push(Item)
remove	--	dequeue()	pop()
size	size()	size()	size()
isEmpty	isEmpty()	isEmpty()	isEmpty()

We will look at each of these types in turn, as well as the fundamental core API. The notion of an API is found in the discussion from page 96-99. Here are the hilights:

These data types were designed to support well-defined behaviors but they also reflect common real-world scenarios. A Queue, for example, is a good way to model a line in a cafeteria. The first one into the line gets the food before everyone else behind him. A Stack can represent the trays in a cafeteria: You grab the topmost tray, which was the last one placed there. Finally a Bag might represent the coins in the cash register. When the cashier wants to grab a quarter, he just grabs one at random from the bin containing all quarters.

Note that these operations mutate the state of the data type in place.

We will be sure to separate discussions of a Data Type from implementation discussions of a Data Structure.

1.3.1 Encapsulation

A well-designed data type does not reveal its implementation, because that is irrelevant to the outside world. It is kept private and hidden. That said, it will always reveal (explicitly or not) its performance, which can be documented. The fundamental principle is to describe the time it takes to perform an operation in relation to the problem size N. We started this discussion on Mar 13 2018 and we will be prepared to complete on Mar 16 2018.

This relates to material found on page 172-177.

1.3.2 Design APIs

A data type is defined by the behavior that it supports. In this regard, an array is not a data type but is a fundamental data structure, much like an int represents 32-bit integers while a long represents 64-bit integers.

Page 97 of the book lists a number of pitfalls when designing the interface to a data type. In many ways, this is an engineering problem, and most people can recognize a well-designed interface when trying to use it for the first time.

We will aim for the following attributes when designing data type interfaces:

• consistency – naming across different types

• completness – there are no missing methods

• testability – satisfactorily validate the correctness of a data type only from its public specification

• empirical validation – devise performance benchmarks to validate the timing specification of API functions.

1.4 Demonstration: Bisection computation

One often needs to compute the root of continuous real functions. The root is where the function f(x) cross the x-axis, or in otherwords, where f(x) = 0. The Bisection method works for continuous functions if you are given two indices, a and b, for which f(a) and f(b) have opposite signs.

See code in algs.experiment.bisection.BisectionMethod.

int signA = (int) Math.signum(f.compute(a)); int signB = (int) Math.signum(f.compute(b)); double c = (a+b)/2; while (Math.abs(b-a) > threshold) { c = (a+b)/2; int signC = (int) Math.signum(f.compute(c)); if (signA == signC) { a = c; } else { b = c; } }

The question to ask is this: How many times does this loop execute?

1.5 Dijkstra’s Two-Stack Algorithm

This algorithm on page 129 uses two stacks to process infix expressions with parentheses.

How do you solve problem "(1 + ((2+3) * (4*5)))"? Observe behavior and discuss.

You must walk through the trace on page 130-131 to verify you see how this algorithm works. On the homework you will see where it breaks down.

Sample Exam Question:

There is an alternate notation known as postfix notation. The above equation would be represented as "1 4 5 * 2 3 + * +". As its name implies, in postfix notation the operator comes after the arguments. Based on the structure of Dijkstra’s algorithm, devise a one stack solution to compute the value of this sequence of tokens.

On the exam, I would ask you to describe this algorithm using pseudocode, which we will be ready to discuss starting Monday.

Note that this is a practical problem. Have you heard of "Postscript"? This is the underyling notation for high-quality documents that, today, are known as PDF documents.

1.6 Stacks appear in many places

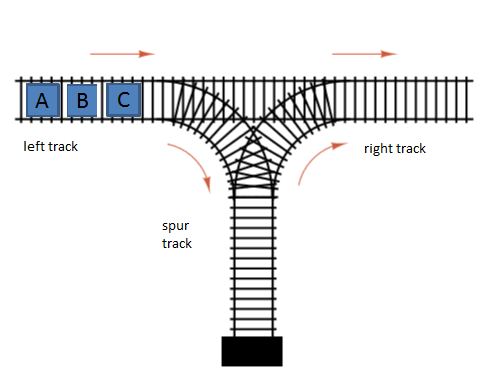
There are three engines on the left "A B C" in that order from left to right. You can move an engine straight through to the right track or it can move onto the spur track. Once on the spur track, the engine can only move onto the right track.

Figure 1: Track Manipulation

What is the only permutation of these three engines that you cannot reproduce on the right track?

1.7 Lecture Takeaways

• Office hours are held in Fuller Sub-Basemenet, FL A22.

• Homework 1 is now published.

• We are working our way up to a cost model for algorithms. For starters, we will assume all basic operations can be performed in constant time. We are concerned with counting loops. We are concerned with operations whose performance depends on the size of a data structure.

• Zoom is available three-times, Sun/Tue/Thur, for online office hours. https://wpi.zoom.us/

1.8 Daily Exercises

I described how the Anagram searcher would use a brute force approach to compute all different possible permutations of the words "GRADS TENSE SHINE" to find a fifteen-letter word.

Can you come up with strategies that might be used to improve the performance of this algorithm, given the above output and the sample list of english words.

1.9 Version : 2018/03/09

(c) 2018, George Heineman