CS 2223 Nov 16 2015

Lecture Path: 12
Back Next

Expected reading: 458-467
Daily Exercise:

For one wild, glad moment we snapped the chain that binds us to earth, and joining hands with the winds we felt ourselves divine...

The Story of My Life
Helen Keller

1 Hashing With Separate Chaining

1.1 HW2 and HW3

Opening discussion of HW2 here. Plus some thoughts on HW3

1.2 Lecture

The Symbol Table (introduced last lecture) represents the ability to store a collection of values to be associated with a given key. The initial implementation stored all (key, value) pairs in a single linked list. This leads to inefficient performance when an increasing number of elements are being stored.

Specifically, when retrieving (get) or inserting (put) a value into the Symbol Table, the performance was directly proportional to the number of elements already stored by the Symbol Table.

We need some way to reduce the length of the linked lists. One solution that works very well in practice is to use a hash function to uniformly partition the keys into different linked lists. This is the intuition and basis for Hashing.

So we start not with a single linked list, but an array of SeparateSearchST objects as we introduced last week. The question remains, however, as to how to partition the keys. The common way to do this is to develop some hashCode method that returns an integer based on the contents of a specific value.

The following is a sample hashCode method for the java.lang.String class:

public int hashCode() { int h = hash; if (h == 0 && value.length > 0) { char val[] = value; for (int i = 0; i < value.length; i++) { h = 31 * h + val[i]; } hash = h; } return h; }

This computed hash value is not guaranteed to be unique. There may be multiple keys that hash to the exact same value. However it is essential that if two key values are equal to each other, then they produce the same hash code.

Each of the fundamentl Java object types (Integer, Double, Float, String) provides a reasonable hashCode method that you can use. For example,

Hello gives 69609650 aaaaaa gives -1425372064

As you can see, sometimes hashCode returns a negative number, because of mathematical overflow – note that hashCode returns an integer.

Now comes the premise, if this hashCode method does a good job in generating uniform integers, then you can create separate SequentialSearchST objects into which to add the (key, value) pairs. But how many objects should we create initially? Instead of worrying too much about that question, start with an initial number, and then resize as needed if the performance begins to suffer.

We are now ready to review the code.

public class SeparateChainingHashST<Key, Value> { int N; // number of key-value pairs int M; // hash table size SequentialSearchST<Key, Value>[] st; // array of symbol tables int INIT_CAPACITY = 4; // initial size int AVG_LENGTH = 7; // Threshold to resize /** Initialize empty symbol table with <tt>M</tt> chains. */ public SeparateChainingHashST(int M) { this.M = M; st = (SequentialSearchST<Key, Value>[]) new SequentialSearchST[M]; for (int i = 0; i < M; i++) { st[i] = new SequentialSearchST<Key, Value>(); } } /** Choose initial default size. */ public SeparateChainingHashST() { this(INIT_CAPACITY); } /** Convert hashCode() into index 0 and M-1 */ int hash(Key key) { return (key.hashCode() & 0x7fffffff) % M; } public int size() { return N; } public boolean isEmpty() { return size() == 0; } public boolean contains(Key key) { return get(key) != null; } public Value get(Key key) { int i = hash(key); return st[i].get(key); } public void put(Key key, Value val) { // double table size if average length of list >= AVG_LENGTH if (N >= AVG_LENGTH*M) resize(2*M); int i = hash(key); if (!st[i].contains(key)) N++; st[i].put(key, val); } }

Important Note: This code is not as efficient as it could be. Discussion Here and explain how this should be different, though it means modifying SequentialSearchST.

Note that this SeparateChainingHashST starts by constructing an array of objects, each of which is a Symbol Table. Whenever a request is made to put a (key, value) into the Hash Table, the appropriate Symbol Table is located by computing the hash code to determine the index i. Then you simply put the (key, value) into that Symbol Table as long as it is not already present.

After a few insertions into a table with M=5 separate chains (you might hear me say the word "bin" or "bucket" since those are common in the literature) you could have the following situation:

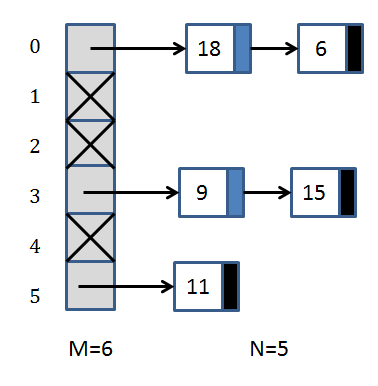
In this case, the hash function is simply "compute modulo 6 of the value being inserted".

1.3 How To Scale

Assuming that the has uniformly distributes key values, this code improves the performance of each operation.

Specifically, when retrieving (get) or inserting (put) a value into the Symbol Table, the performance is now directly proportional to N/M

However, if you do nothing to change the number of M separate chains, you will eventually have decreasing performance, because N will be substantially greater than M.

Much like you have seen before, you need to resize the array of separate chains. However, what to do with the elements that have already been placed into the hash table? It turns out that you have to take a substantial performance penalty hit and reinsert all elements in the hashtable because they may end up in a different index because the value of the hash function is dependent on M.

The following resize method takes advantage of the existing constructor to simplify its implementation. Once done, it updates the st[] array to use the newly created one.

Of the final three statements in the resize method, which one is technically not needed?

// resize the hash table and rehash elements. void resize(int chains) { SeparateChainingHashST<Key, Value> temp = new SeparateChainingHashST<Key, Value>(chains); for (int i = 0; i < M; i++) { for (Key key : st[i]) { // NOTE ITERATOR OVER KEYS temp.put(key, st[i].get(key)); } } M = temp.M; N = temp.N; st = temp.st; }

1.4 How To Iterate

In working on Homework3, you came across the LinkedListIterator which is used to retrieve all of the key values stored within a Symbol Table. This capability increases the convenience of using symbol tables.

Review the code examples to see how this works.

1.5 Demonstration

If you run the SeparateChainingHashST sample code, you will see the following output:

213557 words in the hash table. Table has 45056 indices. there are 392 empty indices 99.1299715909091% maximum chain is 16 number of single is 1841

Note the average number one would expect in a chain is 213557/45056 or 4.74 which is impressive.

These results are incredibly promising! You can determine if an item exists in the Hash Table using no more than 16 comparisons. Even more promising is that for about 1% of the values (1841) you only have to make a single comparison. Of course, the memory requirements are noticeable, but you have to admit this is very nice.

There is a direct comparison to make with using Binary Array Search over a sorted array. First, you would have to sort all strings and construct an array for them. Thereafter, the maximum number of comparisons to locate an entry would be 1 + Floor(log 213557) or 18.

This exercise demonstrates that using additional space can help improve performance.

1.6 Improved Tilde Approximation Explanation

Sometimes when we do Tilde approximation, the goal is to analyze running time performance.

Sometimes we use Tilde approximation to count the number of key operations

Handout and exercise.

1.7 HW2

Homework2 is almost graded; comments will be returned electronically as before. I will make my.wpi.edu announcement with that information.