The preparation for code generation phase decides how to allocate registers and memory. Thhe code generation phase translates the intermediate representation to assembly language using these registers and memory assignments.

Various methods have been developed for good use of registers. One technique is to store all loop variables in registers (until there are no more registers) since statements inside loops may execute more than once.

Another easily implemented technique is to store the variables used the most in registers.

For machines with a stack and a stack pointer, operations involving the stack are generally quicker than those involving an access to (non-stack) memory. Thus, another code generation technique is to push all variables in a procedure onto the stack before the procedure is executed, access them from the stack (and two registers).

Careful assignment of expressions and variables to registers can increase the efficiency of the resulting compiler. In this module, we will generate code as though there were only one available register.

Example 1 shows directives for integers for a number of machines.

Example 1 Directives from a symbol table entry for a name with class = variable, type = integer, and character string A

 	On an 86-family:	A	DW	?
 	On a M68000:		A	DS.L
 

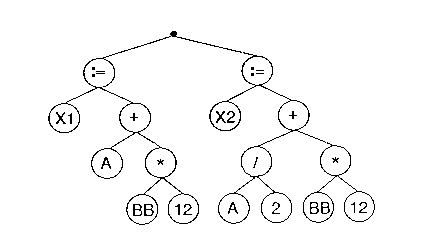
Consider the following abstract syntax tree for the two assignment statements:

X1 := A + BB * 12;

X2 := A/2 + BB * 12;

from Module 1:

Using a tree walk which generates code for the subtrees first, then applies the parent operator, the following code can be easily produced:

Load BB, R1
Mult #12, R1
Store R1, Temp1
Load A, R1
Add Temp1, R1
Store R1, Temp2
Load Temp2, R1
Store R1, X1
Load A, R1
Div R1, #2
Store R1, Temp3
Load BB, R1
Mult #12, R1
Store T4, R1
Load T3, R1
Add T4, R1
Store T5, R1
Load T5,R1
Store R1,X1

For two leaf nodes, the method shown loads the left-most into a register. The right-most leaf node could just as well have been the one put into the register.

Exercise 3 asks the reader to write the algorithm for this method.

Notice that the code continually stores the value in the register into memory in order to reuse it for the next computation. This is called a register spill.

The example in this section generates code for assignment statements whose right-hand sides are expressions. The next section discusses code generation strategies for various other language constructs.

1. Assignment Statements

   A tree pattern of the form:

   

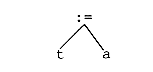
   generates a Move instruction:

   MOVE aPlace,T

   where aPlace represents the register, stack position or memory location assigned to a.

2. Arithmetic Operations

   Suppose Op represents an arithmetic operation and consider an abstract syntax tree for the statement t = a Op b:

   

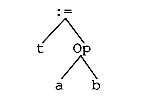
   One possible code sequence is:

    	MOVE	aPlace,Reg
    	OP	bPlace,Reg
    	MOVE	Reg,T
    

   This is the method used in the example of the previous section. Of course, some machines require that special registers be used for operations such as multiplication and division.

   Example 2

3. IF Statements

   IF statements can be represented by an abstract syntax tree such as:

   

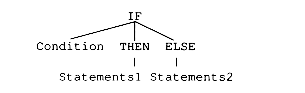
   A typical code sequence is:

    	(Code for condition)
    	BRANCHIFFALSE	Label1
    	(Code for Statements1)
    	BRANCH		Label2
    Label1: (Code for Statements2)
    Label2:
      	
    

   Example 3 illustrates this for the statement:

   IF a < b THEN Max = b ELSE Max = a;

   In Example 3, aPlace and bPlace mey refer to the variables a and b themselves, if the machine allows two memory operands. For machines such as the 86-family (PC-clones) which require that one operand be in a register, the instruction:

   COMPARE aPlace,bPlace

   can be replaced by:
   MOVE Reg,aPlace
CMP Reg,bPlace

   if neither a nor b have been previously assigned to a register.

4. Loops

   Loops are just conditionals whose code is repeated. Consider the loop:

    	LOOP While condition DO
    	   Statements
    	ENDLOOP		
    
    

   An abstract syntax tree is:

   

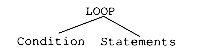
   A reasonable code sequence is:

    Label1:	(Code for NOT condition)
             BRANCHIFTRUE	Label2
    	(Code for Statements)
    	BRANCH		Label1
    Label2:
      	
    

   Example 4 shows such a loop:

   ---

   11.5 Code Generation Techniques

        True code generator generators are still evolving, although much research has been devoted to this topic. Retargetable code generators or table-driven code generators are becoming more common. They enable a code generator to be created for a new machine with relative ease by separating the code generation algorithm (the driver) from the machine description. This is similar to the front-end generators which we saw in earlier chapters.

   ---

   11.6 Register Allocation

   To prepare for code generation, the compiler decides where values of variables and expressions will reside during execution. The preferred location is a register since instructions execute faster when the data referred to in operands reside in registers. Ultimate storage is often a memory location, and due to the scarcity of registers, even intermediate results may need to be assigned memory locations also.

        Memory allocation techniques are discussed in Module 12; in this chapter, we will address the issue of register allocation.

   ---

   11.6.1 Register Allocation vs. Assignment

   The term register allocation is used for two tasks: (1) register allocation itself which decides which program values shall reside in registers and (2) register assignment which picks the specific register in which these values will reside.

        Some compilers make a tentative allocation, then try an assignment, and if necessary reallocate.

   ---

   11.6.2 Register Allocation Schemes

   A good code generator will generate code that minimizes accesses to main memory; it will try to keep as much currently active data (values of variables and expressions) in registers as possible.

        There are two general approaches to register allocation. The first divides the registers to be allocated into two classes. The first class is those globally allocated: those to be allocated for the whole program or for a whole subprogram or perhaps a loop, and the second class is those used for temporary values and computations within a straight-line (no branches from IF's or loops) sequence of code.

        The second method is to do all allocation on a global basis, without dividing the registers into two classes.

        Simple global register allocation allocates registers for variables in inner loops first since that is generally where a program spends a lot of its time. Of course, this same register should be used for the variables if it also appears in an outer loop. After registers have been allocated globally, at least one (and often more) register is kept free for holding temporary results.

   ---

   11.6.3 Register Allocation by Usage Counts

   A slightly more sophisticated method for global register allocation is called usage counts. (This is a heuristic. A heuristic method is one that usually, but not always, makes things better.) In this method, registers are allocated first to the variables that are used the most.

   Example 5

   Consider the following loop:

    	LOOP: X = 2 * E
    	      Z = Y + X + 1
    	      IF some condition THEN
    	        Y = Z + Y
    	        D = Y - 1
    	      ELSE Z = X - Y
    	        D = 2
    	      ENDIF
    	        X = Z + D
                    Z = X
            ENDLOOP
    

   Here, there are five references to X, and Z, five references to Y, three references to D, and one to E. Thus, if there are three registers, a reasonable approach would be to allocate X and Z to two of them, saving the third for local computations. The resulting code would be (something like):

    	Load	X,R1 
    	Load	Z,R2 
    Loop:	Load	E,R3 
    	Mult	#2,R3 
    	Store	R3,X 
    	Copy	R1,R3 
    	Add	Y,R3
    	Add	#1,R3
    	Store   R3,Z
    	IF some condition  THEN
     	  Copy  R2,R3
    	  Add	Y,R3
              Store R3,Y
    	  Load	Y,R3
    	  Sub   #1,R3
    	  Store R3,D
    	ELSE Copy R1,R3
    	  Sub	Y,R3
    	  Store R3,Z
    	  Load  #2,R3
        	  Store R3,D
            ENDIF
    	  Copy  R2,R3
              Add   D,R3
              Store R3,X  
              Store R3,Z
    {ENDLoop}
    

   ---

   11.6.4 Register Allocation by Graph Coloring

   Using data flow of uses and definitions of variables, set up use-def chains:
   A Use of a variable A is reached from the assignment A = if there is some path from the assignment along which A is used before being redefined.

   Link a def with all its uses to form a chain

   Two program quantities cannot share the same register if their use-def chains overlap.

   Called Overlapping lifetimes

   Algorithm

   Register Allocation by Coloring

   For each program quantity to be allocated to a register,
Create A Node
Draw an arc between nodes whose lifetimes overlap
Colorgraph(n)


   Called an Interference Graph

   If n registers, and graph can be colored with n colors, registers can be assigned.

   An NP-Complete Problem

   ---

   11.6.5 Register Assignment and Reassignment

   Register Allocation prioritizes which variables to be kept in registers

   Register Assignment (the other side) Which actual registers to use

   May depend on the machine

   Registers allocated and then freed

   Register spill: when we remove a value we'd really like to keep in a register, but can't

   Small constants

   Stored value same

   Variables and expressions not "live"

   Heuristics

   Algorithm

   Belady's Algorithm adapted for Register Allocation

   If the required value is already in a register, then leave it there.

   Create A Node

   Else if there is an acceptable register, use it

   Else use that register whose value won't be used for the longest time (spill the value)

   ---

   11.6.6 Register Management

   Lots of bookkeeping for overseeing registers. Useful info to keep:
   Description of contents

   Future uses (usage counts)

   Distance to next use

   Copy in memory?

   Copy in another register

   Cost of recomputing contents

   Most recent use

   Past uses

   ---

   11.7 An Efficient Register Allocator and Code Generator

   The following algorithm writes on each tree node of an expression tree the number of registers needed to compute the node. It assumes a computer model that keeps one of its operand in a register. Left-most leaves are assigned a "1", and right-most leaves are assigned a "0" to allocate registers (it could be reversed). Parent nodes are assigned the maximum of the values of both children. If the values are equal one more register is needed to store the result, so the parent node is assigned the (equal) value plus one.

    
    	Algorithm 
    	Label (Expression Node) 
    	
    	1. Node is a left-most leaf: Label   = 1
    	2. Node is a right-most leaf: Label   = 0
    	3. (Otherwise) 
    	    3(a)Label (Left(Node)
    	    3(b)Label (Right(Node)
    	    3(c)Label# (Node) = Max(Left Label# , Right Label#)
    	        or Left Label# + 1 if Left Label# = RightLabel#.
    
    
    

   The algorithm is called with Label(root)

   Using the tree labelled as above, we can write an effiecient code generation algorithm:

    
    
    	
    	Algorithm 
    	GenerateCode (Node) 
    	CASE Node is:
    
      		A leaf labeled 1 and a left leaf:
    		   (a) R = GetReg
    		   (b) Generate "Load Node, R"
    	        Labeled with a number greater than available registers:
    		   (a) Generate code for right child
    	           (b) Store the result in a temp
    	           (c) Generate code for the left child
                       (d) Apply node's  operator to (a) and (c)
    	        Has a right child that is a leaf:
    	           (a) Evaluate the left child
    	           (b) Apply node's operator to left child
                           result and leaf.
    	        Otherwise:
    		   (a) GenerateCode(Node with larger label). (Use either if
    	               labels are the same) Leave result in a register
    		   (b) GenerateCode (Other Node)
    	           (c )Apply node's  operation to registers holding
                           the two results.
    
    
    
    

   ---

   11.8 Code Generation from DAG's

   The optimal code generation algorithm is an NP-complete problem. Directed acyclic graphs allow a code Generation heuristic:
   Put out code for each node immediately after code for its children has been emitted as far as possible because then the results are more apt to still be available, say in a register.

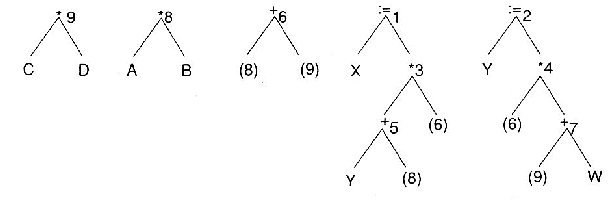
   To prepare the list of DAG nodes to compute (that is, the list for which code is to be emitted), start at the root of the right-most subtree. Put this node on the list, L, and continue by adding a left-most node to the list after all its parents are already on the list. Then generate code for the nodes in L by starting at the end of L and proceeding to the beginning.

   Example 10
   Generating code from a DAG

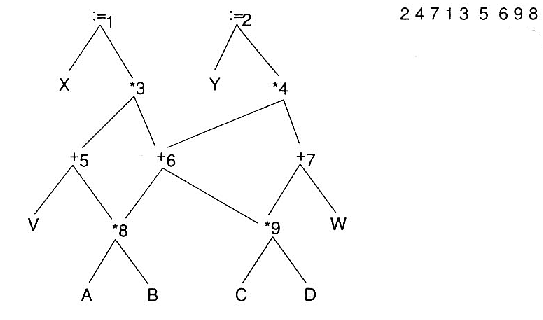
   Thus, we would put out code for node 8 first, then node 9, etc.

   Another way to put out good code from DAG's is to break the DAG up into trees and to use a code generation algorithm which is optimal on trees. (Of course, it takes time to break up the DAG.)

   Example 11
   Breaking DAG's into trees

   ---

   11.9 Retargetable Code Generation

   Retargetable code generation is a step towards automatic code generation. The code generator is designed so that it can be changed to produce code for a new machine. These may be categorized (Ganapathi et al., 1982) as (1) interpretive code generators, (2) pattern matching code generators and (3) table-driven code generators. In all of these, an attempt is made to separate the code generation algorithm from the machine code itself. This fits our model of a driver and the information on which the driver operates with the code generation algorithm analogous to the driver.

   ---

   11.10 Peephole Optimization

   Peephole optimization is actually a family of optimizations that looks at a small number of outlines of output code, looking for a pattern. It is so easy to do many of these that it is not unreasonable to put out poor code initially. It simplifies the code generation phase. Compiler designers look at the code produced when a compiler is up and running. This is called profiling. As they find new patterns actually produced, they keep adding optimization routines.

   ---

   11.10.1 Unnecessary Loads

   Consider the following code sequence:
   STORE REG1, A

   LOAD A, Reg2

   Clearly, A is still in a register and there is no need to reload it into register 2.

   ---

   11.10.2 Branch (to a) (around a) Branch

   Many times compilers produce code that branches to another branch. Consider the following embedded CASE statements and the branches produced by a simple code generator:

    

   Line Source	Output Code
   50 WHILE a DO	50:
   51 BEGIN
   ...
   61 CASE i OF
   62 0: IF b THEN
   63 x:=1;
   64 ELSE	64: BRANCH 66
   65 x:=2;
   66 {end case i=0}	66: BRANCH 142
   67 l:
   ...
   81 4: CASE j OF
   ...
   89 2: IF b THEN
   90 x:=0;
   91 ELSE	91: BRANCH 93
   92 x:=1;
   93 {end case j=2}	93: BRANCH 121
   ...
   120 end; {case j}
   121 {end case i=4}	121: BRANCH 142
   ...
   141 end; {case i}
   142 end; {while a}	142: BRANCH 50

   Just looking at the BRANCHes, we see:

   50:

   64: BRANCH 66

   66: BRANCH 142

   91: BRANCH 93

   93: BRANCH 121

   121: BRANCH 142

   142: BRANCH 50

   If we fully eliminated the indirect jumps, it would look like this:
   50: 64: BRANCH 50

   66: BRANCH 50

   91: BRANCH 50

   93: BRANCH 50

   121: BRANCH 50

   142: BRANCH 50

   ---

   11.10.3 Cross-Jumping

   IF-THEN-ELSE statements often produce almost duplicate code within the THEN and ELSE clauses. Consider the following:
   IF Condition THEN
   A[I]:=x+1

   ELSE

   A[I]:=y+1

   The output code differs by only 1 load. We can perform that load and then execute the rest of the instructions: ADDing 1 and assigning to A[1]. This can be seen pictorially where test is the code for the condition:

   

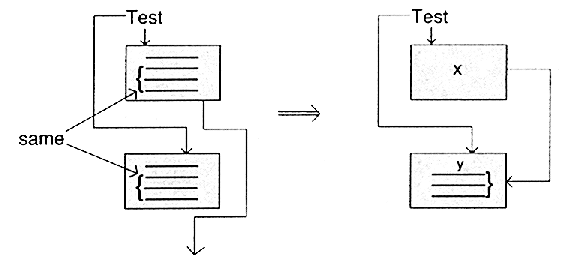
   In the right-most picture the identical code is written only once.

   ---

   11.10.4 Recognizing Special Instruction or Modes

   Instructions that ADD one can often be replaced by an increment (for machines that have and increment instruction)
   ADD #1, Reg2

   may be substituted with
   INCREMENT Reg2

   Sometimes instructions can be combined be looking for the longest number of operators that can be turned into a single instruction. For example,
   ADD Reg1, Reg2

   MOVE Reg2, A

   can be changed on some machines to
   ADD Reg1, Reg2, A

   Clearly, these cases are both source language dependent and machine dependent.

   ---

   11.11 Summary

   Code generation translates the intermediate representation of a program to executable code, while symbol table information is often translated to the storage allocation directives of a machine. The resulting instructions should be spaced and time efficient. Since resources such as registers are limited, choices are made when there is more than one way to perform the same computation.

   A statement by statement code generator tends to produce poor code, where by "good" code we mean code that executes fast or takes up less space. To produce better code, code generation avoids extra computation, reusing computed values (common subexpressions) if reuse is less expensive than recomputing.

   Further efficiency can be achieved by avoiding extra loads, unnecessary stores, avoidable register-to-register moves, and special instructions.

   A good code generator design, like all software, is easier to implement, easier to test, and easier to maintain.