| 6.0 Introduction
6.4 Semantic Analyzer Generators |
6.5.5 Absolutely
Noncircular Attribute
Grammars
In Section 6.6 we present some efficient attribute evaluation methods. One of them requires that the attribute grammar be noncircular in an even stronger way than the noncircular definition above.
We start with the dependency graphs for the productions of a grammar. Figure 2 shows the nodes of the dependency graph for the binary digit grammar.
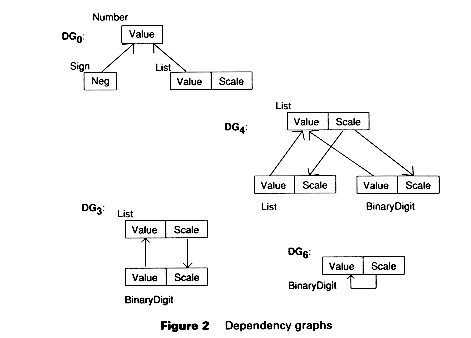
Example 8 shows these graphs merged to create the dependency graph for a parse tree, T. List's Scale attribute is handed down the tree to the BinaryDigit node where it is used to calculate the value of Scale. This value is handed back up the tree, changing as it goes, but ultimately it is used to calculate List's Value attribute. In functional notation, we would write:
List.Value = f
(List.Scale)
where function, f (the accumulation of the changes to Scale as it descends the tree), is used to compute Value and then is handed back up to the node. We indicate these closure steps by drawing an arc in the list node labeled with an asterisk, and we label the nodes themselves with asterisks, calling the new graph augmented dependency graphs.
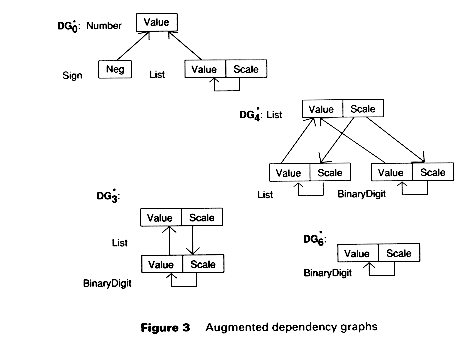
With augmented dependency graphs defined, we can define absolute noncircularity. An attribute grammar is absolutely noncircular if none of the augmented dependency graphs, DG*p, contains a cycle.
Absolute noncircularity is a stronger restriction than noncircularity.

![]()