| 6.0 Introduction
6.4 Semantic Analyzer Generators |
6.5.4 Noncircular Attribute Grammars
If the calculation of an attribute comes around to using its own value in the calculation, then we have a circularity. We will, however, need a more formal definition of circularity in terms of dependency graphs.
Dependency Graph of a Production
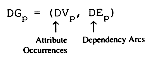
The dependency graph of a production, p, is a set of vertices and edges. The vertices are the attribute occurrences (see Section 6.1.1) and the edges are dependencies.
Formally, for each production
p: Xo![]() X1 X2. . . Xn,
X1 X2. . . Xn,
DVp = { (a, k) | a is in A(Xk), 0<=k<=n }
and
DEp = {<(b, i) ,(a, k)>
| < (b,i) is in Dp(a, k)}
Thus, if O1 is in the dependency set for O2, then there is an arc between attribute occurrence O1 and attribute occurrence O2.
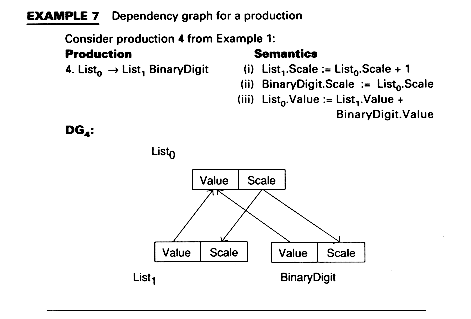
In Example 7,
DV4 = { (Value, 0), (Scale, 0), (Value, 1), (Scale, 1), (Value, 2), (Scale, 2) }
DE4 = { <(Value, 1), (Value, 0)>, <(Scale, 0), (Scale, 1)>, <(Value, 2), (Value, 0)>, <(Scale, 0), (Scale, 2)> }
The dependency graph for an input program is produced by merging the dependency graphs for each production used to parse the program. It is defined in terms of the parse tree, T.
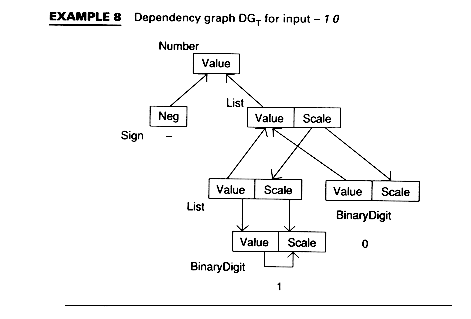
Since the dependency graph for an input is defined by augmenting the nodes of the parse tree with attributes, the definition of noncircularity is in terms of this parse tree:
An attribute grammar G is noncircular if there does not exist even one tree, T, such that DGT contains a cycle.
Attribute grammars which are circular are undesirable. Knuth (1968, 1971) presents an algorithm which tests a grammar for noncircularity. It is exponential in the worst case. Jazayeri et al. (1975) show that there is no algorithm that tests a grammar for circularity which is not exponential in the worse case. Fortunately, most grammars do not exhibit this worst case behavior.
![]()