|
| 6.0 Introduction
6.4 Semantic Analyzer Generators |
6.5.1 Fundamental Definitions
As we know, an attribute grammar is a context-free grammar to which attribute and semantic functions have been added:
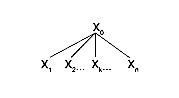
Consider a production p in the set of production P :
p : X0 
X1 X2 X3. .
. Xn n
> = 1
For any Xi in the production p, there may be finite disjoint sets I(Xi) and S(Xi.) The are the inherited attributes and synthesized attributes, respectively.
In general, the values of inherited attributes are passed down the parse tree. The value of synthesized attributes are passed up the parse tree.
The set of all attributes for X i is denoted A(Xi):
A(Xi) = I(Xi)
U S(Xi)
An attribute a of Xi is denoted Xi.a whether it is a reference to attribute a in the parse tree or the grammar.
Predefined attribute values are called intrinsic. Synthesized, intrinsic attributes of terminals are computed by the lexical analysis phase. Inherited intrinsic attributes of the start symbol are passed as parameters before evaluation begins from the parser.
A production p : X0 X1 X2 X3. .
. Xn possesses an attribute occurrence, (a, k), if Xk is at
node #m ( in some tree-numbering scheme), then we say Xk possesses an attribute
realization, (a, m), if Xk has an attribute a. A semantic
function, sometimes called an attribute rule, gives a value to an attribute occurence(a,
k), in production p. Such a function is denoted fp(a,k)
The set of values upon which fp(a,k)depends is called the dependency set for (a, k) and is denoted Dp(a,k). Thus,
Dp(a,k)
= { (b, j) | fp(a,k) = g (. . .Xj.b, .
. . ) }
This is read "the value of attribute occurrence (a, k), or Xk. a depends on the set of attributes { (b, j) } or { Xj.b } where each Xj.b is used in the calculation of Xk. a".
Example 1 illustrates these definitions. This example is an adaptation from Knuth (1968) where he first defined attribute grammars.
The attributes in Example 1 are:
I (Number)
= 
I (Sign)
=
I (List)
= {Scale}
I (BinaryDigit)
= {Scale}
S (Number)
= { Value }
S (Sign)
= { Neg }
S (List)
= {Value }
S (BinaryDigit) = {Value }
Thus, Scale is an inherited attribute, and Value and Neg are synthesized attributes. The intrinsic attributes are Sign.Neg in productions one and two, BinaryDigit.Value in production five, and List.Scale in production zero.
The function to compute List0.Value in production four is denoted f4(Value, 0).
Since depends List0.Value depends on List1.Value and BinaryDigit.Value,
D4(Value,
0) = { (Value, 1 ) , (Value, 2) }
Example 1 generates strings of binary digits. Example 2 shows an unevaluated parse tree for the string - 1 0:
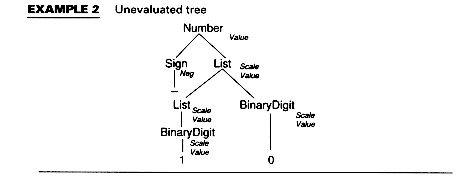
Section 6.6 discusses efficient methods for attribute evaluation, but we can "guess" at a method here: since we know value is a synthesized attribute, and Scale is an inherited attribute, we can try to evaluate values by moving up the tree, then down, or by moving down the tree, then up. The latter suffices, and Example 3 shows the evaluated tree.
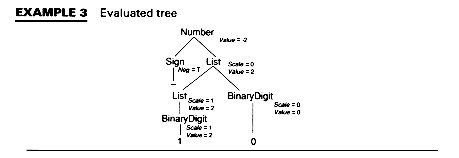
Example 3 shows that the "semantics" of this example computes the decimal value of the string and leaves this value at the root of the tree.
Example 1 through 3 are a short and simple illustration of attribute grammars. It is possible to evaluate all the attributes in one pass down and then up the parse tree.
When a grammar is large and contains many attributes, it is not always easy to see how to evaluate the attributes. One method is to restrict the form of the attributes and attribute functions so that the method of evaluation is known. A second way is to create a graph of dependencies and check to see that it has no cycles. If it has no cycles, the dependency graph itself can be used to give an order in which to evaluate the attributes. We discuss all of these in the next sections.
Example 5 shows calculation of array offsets. This calculation might be performed in order to allocate the relative position of each array element.
Exercise 5 asks the reader to create attributes that will pass information about the array A (the dimensions d1, d2, d3) down the tree and then to calculate this offset while reascending the tree. Exercise 6 asks the reader to consider a different grammar for this same example.
