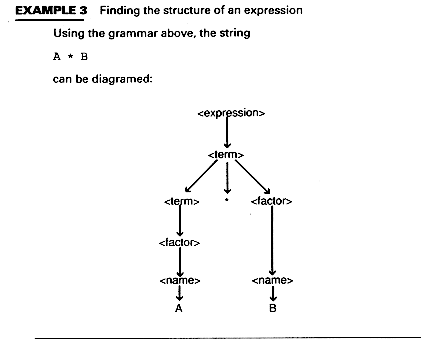
 Parse Tree for A * B
A parse tree shows the structure of a string using the grammar.
Parse Tree for A * B
A parse tree shows the structure of a string using the grammar.
Other ways to describe this aspect are to say that the language should have an inherent simplicity and be easy to learn, expressive and orthogonal. Expressiveness is the power of a language to solve problems. Orthogonality requires combinations of legal constructs to be themselves legal constructs. For example, if a user type of stack is created, and the language allows arrays, an array of stacks would also be allowed. This feature is somewhat related to the object-oriented concept polymorphism and to the concept of first-order languages.
Included in the mathematical aspect is the ability of the language's syntax and semantics to be described accurately and precisely
The time to construct the compiler and its size and speed as well as its "user-friendliness" are all factors to be considered. The original FORTRAN compiler took 18 person-years to develop! We can now design and implement a compiler much faster because tools to generate various phases have been developed and becuase algorithms and data structures for the various compiler tasks have been developed.
The time to construct the compiler and its size and speed as well as its "user-friendliness" are all factors to be considered. The original FORTRAN compiler took 18 person-years to develop! We can now design and implement a compiler much faster because tools to generate various phases have been developed and becuase algorithms and data structures for the various compiler tasks have been developed.
Stated more mathematically, a grammar is a formal device for specifying a potentially infinite language in a finite way, since it is impossible to list all the possible strings in a language whether it is English or C. At the same time, a grammar imposes a structure on the sentences in the language. That is, a grammar, G, defines a language, L(G), by defining a way to derive all legal strings in the language. We will look at this for a (very) small subset of English.
<sentence> -- > <noun phrase> <verb phrase>
<noun phrase> -- > <adjective> <noun phrase>
| <adjective> <singular noun>
<verb phrase> -- > <singular verb> <adverb>
<adjective> -- > a | the |little
<singular noun> -- > boy
<singular verb> -- > ran
<adverb> -- > quickly
Here, the arrow, -- >, might be read as "is defined as" and the vertical bar,
"|", as "or". Thus, a noun phrase is defined as an adjective
followed by another noun phrase or as an adjective
followed by a singular noun. This definition of
noun phrase is recursive because noun phrase occurs
on both sides of the production. Grammars are recursive to allow for
infinite length strings. This grammar is said to be context-free because only one syntactic category, e.g., <verb phrase >, occurs on the left of the arrow. If there were more than one syntactic category, this would describe a context and be called context-sensitive.
A grammar is an example of a metalanguage- a language used to describe another language. Here, the metalanguage is the context-free grammar used to describe a part of the English language.
Example 2 shows a diagram called a parse tree or structure tree for the sentence the little boy ran quickly.
The sentence: "quickly, the little boy ran" is also a syntactically correct sentence, but it cannot be derived from the above grammar. In fact, it is impossible to describe all the correct English sentences using a context-free grammar.
On the other hand, it is possible, using the grammar above, to derive the syntactically correct, but semantically incorrect string, "little the boy ran quickly." Context-free grammars cannot describe semantics.
<expression> ::= <expression> + <term> | <term>
<term> ::= <term> * <factor> | <factor>
<factor> ::= ( <expression> )
| <name> | <integer>
<name> ::= <letter> | <name> <letter> | <name> <digit>
<integer> ::= <digit> | <integer> <digit>
<letter> ::= A | B | ... |Z
<digit> ::= 0 | 1 | 2 | ... | 9
Here, we have used "::=" for is defined as rather than an arrow,
-- > as before. The metalanguage BNF (Backus-Naur Form) is a way of specifying
context-free languages, and BNF was originally defined using ::= rather than -- >. As long as we understand what is meant and what the capabilities of this
grammatical notation are, the notation doesn't matter. We will often omit
the angle brackets, < >, when writing BNF.Unlike natural languages like English, all the legal strings in a programming language can be specified using a context-free grammar. However, grammars for programming languages specofy semantically incorrect strings as well. For example context-free languages cannot be used to tell if a variable, say, A, declared to be of type boolean is used in an arithmentic expression A + 1.
 Parse Tree for A * B
A parse tree shows the structure of a string using the grammar.
Parse Tree for A * B
A parse tree shows the structure of a string using the grammar.
(E stands for expression, T for term and F for factor. The number above each arrow is the number of the production applied.
A left derivation replaces the left-most nonterminal at each step of the derivation, while a right derivation replaces the right-most nonterminal at each step


 Terminals
Terminals
 Nonterminals
Nonterminals
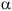
or
A -- > 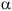
where A is a nonterminal and 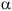 is a string of terminals and nonterminals. In the Expression grammar
E -- > E + T is a production.
is a string of terminals and nonterminals. In the Expression grammar
E -- > E + T is a production.
 Sentential Form
Sentential Form
 Sentence
Sentence
Algorithm
Derive String
String := Start Symbol
REPEAT
Choose any nonterminal in String.
Find a production with this nonterminal on the left-hand side.
Replace the nonterminal with one of the options on the right-hand
side of the production.
UNTIL String contains only terminals.
T -- > F {* F}
F -- > (E) | a
Of course, since F can derive an E in F -- > (E), this grammar is still (indirectly) recursive.
T -- > F {* F}
F -- > (E) | a
Of course, since F can derive an E in F -- > (E), this grammar is still (indirectly) recursive.
Similarly, meaning is assigned to programming language constructs based on their syntax. We prefer, therefore that programming language grammars describe programs unambiguously.
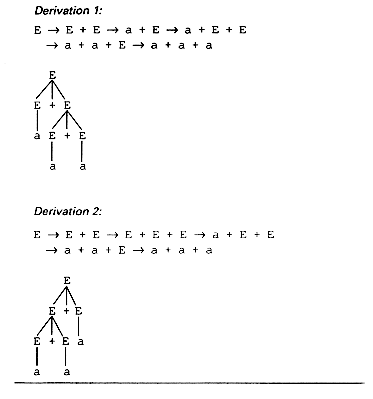
A sentence is ambiguous if there is more than one distinct derivation. If a sentence is ambiguous, then the parse tree is not unique; we can create more than one parse tree for the same sentence.
A grammar is ambiguous if it can generate even one ambiguous sentence.
E -- > E * E
E -- > (E)
E -- > a
|IF b THEN S
|a
where b represents a boolean condition and a
represents some other statements. Then
S -- > IF b THEN S ELSE S
has two parse trees. 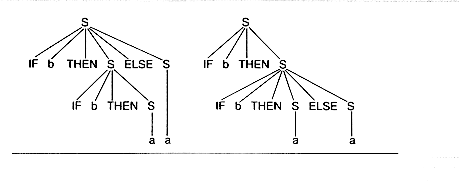 IF b THEN IF b THEN a ELSE a
IF b THEN IF b THEN a ELSE a
The second parse, with ELSE associated with the closest IF is considered the way this should be parsed.
We can rewrite this grammar to be unambiguous:
S2 -- > IF b THEN S2 ELSE S2 | a
Then,
S1 -- > IF b THEN S1 | IF b THEN S2 ELSE S1 | a
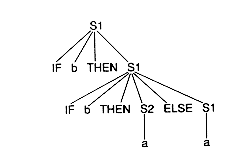
IF b THEN IF b THEN a ELSE a has only 1 parse
A string may be derived from its grammar. Parsing is the process of "discovering" a derivation, given an input string and a grammar.