CS 542. Fall 2001

Homework 7.

Assigned: Tuesday, 27th Nov. 2001
Due: Tuesday, 4th Dec. 2001
Maximum: 100pts.
Purpose of homework: To become familiar with file organizations, indexes, sorting and query processing.
NOTES: This homework is to be done by an individual student, no team work allowed. 

Problem 1: [ 15 pts ]

Consider a relation stored as a randomly ordered file for which the only index is an unclustered index on a field called sal. 

  1. If the most frequently issued query is based on the predicate sal=20, which indexing technique you will use for the index? Explain?
  2. If you want to retrieve all records with sal>20, is using the index always the best alternative? Explain.
  3. If you have to use the index to retrieve all records with sal>20, how would you do to reduce file I/O's.

Problem 2: [ 25 pts ]

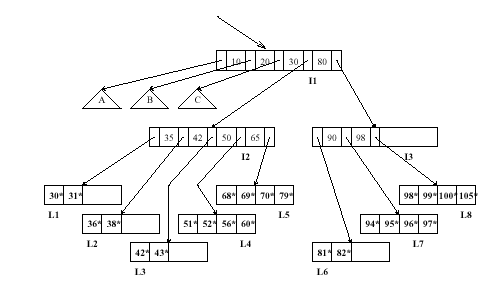
Consider the B+ tree index shown in the following figure, which uses Alternative (1) for data entries. Each intermediate node can hold up to five pointers and four key values. Each leaf can hold up to four records, and leaf nodes are doubly linked as usual, although these links are not shown in the figure (refer to textbook Fig. 9.29.)

 

Answer the following questions. 

  1. Name all the tree nodes that must be fetched to answer the following query: Get all records with search key greater than 38." 
  2. Insert a record with search key 109 into the tree. Show in a figure those nodes changed. 
  3. Delete the record with search key 81 from the (original) tree. Show in a figure those nodes changed. 
  4. Name a search key value such that inserting it into the (original) tree would cause an increase in the height of the tree.
  5. Note that subtrees A, B, and C are not fully specified. Nonetheless, what can you infer about the contents and the shape of these trees? (Hint: in terms of heights and range of key values.)

Problem 3: [ 20 pts ]

Assume that you have just built a dense B+ tree index using Alternative (2) on a heap file containing 20,000 records. The key field for this B+ tree index is a 40-byte string, and it is a candidate key. Pointers (i.e., record ids and page ids) are (at most) 10-byte values. The size of one disk page is 1,000 bytes. The index was built in a bottom-up fashion using the bulk-loading algorithm, and the nodes at each level were filled up as much as possible. 

Answer the following questions.

  1. How many levels does the resulting tree have? 
  2. For each level of the tree, how many nodes are at that level? 
  3. How many levels would the resulting tree have if key compression is used and it reduces the average size of each key in an entry to 10 bytes? 
  4. How many levels would the resulting tree have without key compression, but with all pages 70 percent full?

Problem 4: [ 20 pts ]

Suppose that you have a file with 10,000 pages and that you have five buffer pages. Answer the following questions for each of these scenarios, assuming that our most general external sorting algorithm is used:

  1. How many runs will you produce in the first pass? 
  2. How many passes will it take to sort the file completely? 
  3. What is the total I/O cost of sorting the file? 
  4. How many buffer pages do you need to sort the file completely in just two passes?

Problem 5: [ 20 pts ]

Consider the join R R.a=S.bS, given the following information about the relations to be joined. 

The cost metric is the number of page I/Os unless otherwise noted, and the cost of writing out the result should be uniformly ignored.

Answer the following questions.

  1. What is the cost of joining R and S using a page-oriented simple nested loops join? 
  2. What is the cost of joining R and S using a block nested loops join? 
  3. What is the cost of joining R and S using a sort-merge join? 
  4. What is the cost of joining R and S using a hash join?