cs2223 Problem 1 Solution

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Problems] [Problem 1]

cs2223, D97/98 Problem 1 Solution

Problem 1_1

A program which performs n-digit doubling is contained in the CCC directory

/cs/cs2223/problems/problem1/problem1_1

A README file explains how the program works and it contains a listing of the output, which shows that the number of multiplies is linear in n.

Problem 1_2

The best case of the insertion sort is an inversely-sorted array (large numbers come first) - the sorting is linear in n. The worst case is a sorted array (smallest numbers come first) - it is approxmiatelyof order n²/2. The average case, is s approxmiatelyof order n²/4. A program which performs insertion sorting is contained in the CCC directory

/cs/cs2223/problems/problem1/problem1_2

A README file contains the detailed calculation. It also explains how the program works and contains a listing of the output, which verifies the calculated results..

Problem 1_3

To put the nine functions in their proper order, eight binary comparisions - or pairs of binary comparisions - have to be made. They can be done in any order. Here they are in the order shown in the problem set.

Comparison 1

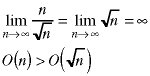
lim(n->infinity; n/sqrt(n)) = lim(n->infinity; sqrt(n)) = infinity; O(n) > O(sqrt(n))

Comparison 2

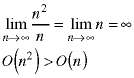
lim(n->infinity; n^2 / n) = lim(n->infinity; n) = infinity; O(n^2) > O(n)

Comparison 3

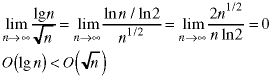
lim(n->infinity; lg(n)/sqrt(n)) = lim(n->infinity; (ln(n) / ln(2)) / sqrt(n)) = lim(n->infinity; 2*sqrt(n)/(n*ln(2))) = 0; O(lg(n)) < O(sqrt(n))

Comparison 4

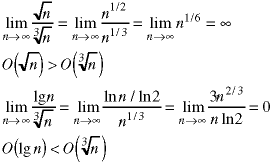
lim(n->infinity; sqrt(n) / n ^ (1/3)) = lim(n->infinity; n^(1/2) / n^(1/3)) = lim(n->infinity; n^(1/6)) = infinity; O(sqrt(n)) > O(n^(1/3)); lim(n->infinity; lg(n) / n^(1/3)) = lim(n->infinity; (ln(n) / ln(2)) / (n^(1/3))) = lim(n->infinity; 3 * n^(2/3) / (n * ln(2))) = 0

Comparison 5

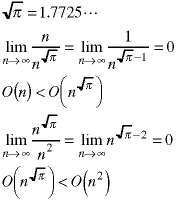
sqrt(pi) = 1.7725.... ; lim(n->infinity; n / n^(sqrt(pi))) = lim(n->infinity; 1 / n ^ (sqrt(pi) -1)) = 0; O(n) < O(n ^ sqrtt(pi)); lim(n->infinity; n^sqrt(pi) / n^2) = lim(n->infinity(n^(sqrt(pi) -2)) = 0; O(n^sqrt(pi)) < O(n^2)

Comparison 6

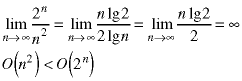
lim(n->infinity; 2^n / n^2) = lim(n->infinity; (n*lg(2)) / (2*lg(n))) = lim(n->infinity; n*lg(2)/2) = infinity; O(n^2) < O(2^n)

Comparison 7

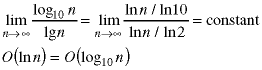
lim(n->infinity; log(10; n) / lg(n)) = lim(n->infinity; (ln(n) / ln(10)) / (ln(n) / ln(2))) = constant; O(ln(n)) = O(Log(10; n))

Comparison 8

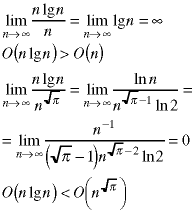
lim(n->infinity; n*lg(n)/n) - lim(n->infinity; lg(n)) = infinity; O(n*lg(n)) > O(n); lim(n->infinity; n*lg(n)/n^sqrt(pi)) = lim(n->infinity; ln(n) / (n^(sqrt(pi) -1) * ln(2))) = lim(n->infinity; (1/n) / ((sqrt(pi) -1) * n^(sqrt(pi) - 2) * ln(2)) = 0; O(n*lg(n)) < O(n^sqrt(pi))

Combining everything,

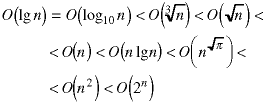
O(lg(n)) = O(log(10: n)) < O(n^(1/3)) < O(sqrt(n)) < O(n) < O(n(lg(n)) < O(n^sqrt(pi)) < O(n^2) < O(2^n)

Grading

The grading criteria are available. These are subject to interpretation by the grader. As we stated in class, our primary goal in the grading of these exams is consistency. If your intrepretation differs from the grader's and the grader has applied her/his criteria uniformly, then the grader's interpretation will prevail.

[cs2223 text] [News] [Syllabus] [Problems] [Problem 1]

Contents ©1994-1998, Norman Wittels
Updated 27Mar98
Updated 26Mar98