cs2223 Exam 1

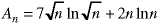
[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Exams]

cs2223, D97/98 Exam 1

Go to Solution

Question 1.1

The number of additions performed an algorithm when working with an array of size n obeys this equation;

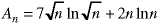
A(n) = 7 * sqrt(n) * ln(sqrt(n)) + 2 * n * ln(n)

What is the order of the algorithm O(A_n)?

Question 1.2

The mathematical constant e can be expressed as an infinite series:

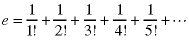
e = 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + ...

The denominators are just the factorials of the integers:

1! = 1, 2! = 1*2, 3! = 1*2*3, 4! = 1*2*3*4, ...

Let En represent the error which results from truncating the series to length n. For example the third element in the sequence is:

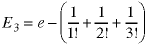
E(3) = 3 - (1/1! + 1/2! + 1/3!)

2a). Write an expression for E_n which does not contain e. It can, however, contain summations.

2b) Write a recurrence relation for E_n. You don't have to solve it, but you do have to show your mathematical derivation.

Question 1.3

Pascal's triangle plays an important role in understanding binomial relations. Each element is formed from the sum of the numbers above it and the one to the upper left if it. We want to calculate C_n, which tells how many numbers are contained in a Pascale triangle with n rows. This example shows that C₅, =15.

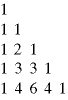
The first 5 rows are, 1, 11, 121, 1331, 14641

3a) Write a recurrence relation for C_n.

3b) We guess that the solution to the recurrence relation is

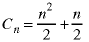
C(n) = n^2/2 + n/2

. Prove or disprove whether this guess is correct.