cs2223 Class 26

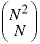
[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 26

N-queens

In Class 24 we introduced the N-queens problem. In this class we discuss how to solve it and related problems.

If there are N² squares on the chessboard and N queens, there are

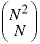
C(N^2, N). C is the

ways to place the queens. Most are not solutions to the problem. We could just calculate them all and throw aways non-solutions. Unfortunately, this is a large number. For a standard 8x8 chessboard, it is

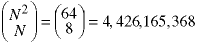
C(N^2, N) = C(64, 8) = 4,425,165,368

This number grows very rapidly with N.

We can reduce the number of cases by noticing that the solution will contain no two queens in the same row or column. Thus we can create a vector of column numbers:

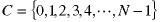
C = {0, 1, 2, 3, 4, ... , N-1}

Then each permutation of this vector represents a different arrangement of the queens - it tells us column number of the queen in each row:

for 0 <= k < N, row(k) = k, col(k) = C[k]

Since there are N! permutations of the vector, that is the number of possible chessboard arrangements. For a standard chessboard, this is:

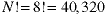
N! = 8! = 40,320

That is better, but we still need a way to find (and eliminate) trial solutions.

Permutations

First, we look at a recursive way to calculate the permutations of the vector C. We use this function

permute(int start, int length, int *vector);

Which starts at some position 0 <= k < N in the vector and permutes what comes after it:

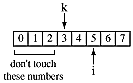
Figure showing the vector {0, 1, 2, ... , 7}. The elements 0-7 are marked 'don't touch these numbers', k points to the element 3 and i points to the element 5

This is done by sequentially swapping k with each k <= i < N , permutting everything to the right of k, then swapping back. Here are the first few operations of this algorithm.

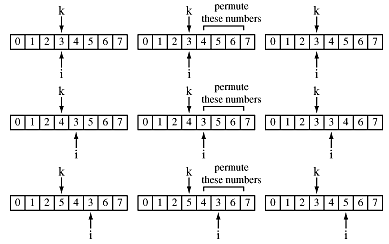
And here is the code for the function.

void permute(int k, int n, int *vec) // calculate permutations of a vector
	{ // n is the length of the vector, k is the position to begin permutations
	if (k >= n-1) return; // permutation is complete
	for (int i = k; i < n; i++)
		{
		int temp = vect[k]; vect[k] = vect[i]; vect[i] = temp; // swap
		permute(k+1, n, vect); // recursive call
		temp = vect[k]; vect[k] = vect[i]; vect[i] = temp; // swap back
		}
	} // end permute()

The attached script shows that this function produces the proper results. Note, the first line in the program can be uncommented to print ou the values, as shown in this script. But, be careful. The number of printed lines can be quite large.

N-queens algorithm

The N-queens algorithm does the following:

Create the column numbers vector of the proper length
For each permutation of that vector, check that no queen in on a diagonal with the queens above it.

This algorithm is of order O(N!) because that's how many permutations there are. The actual number is somewhat less since the algorithm terminates once the first solution is found. We can speed up the algorithm somewhat by noting that any partial solution (we're checking one of the middle queens) only works if the queens above it already have successfully passed the "no diagonals" test. So, we modify our algorithm:

Create the column numbers vector of the proper length
For each permutation of that vector, check that no queen in on a diagonal with the queens above it.
Any time a diagonal conflict is found, stop the current permutation and back up one level.

The diagonal tests

Figure showing a portion of a chessboard witha queen in row k and column C[k]. In terms of the C[k] vector, k points to an element. Everything to the left is the queens above it; everything to the right will be later queens - they can be ignored.

We only have to look at the rows above the queen we are trying to place - that means we only need to look at values of C which come before C[k]. If the queen in the row above is on the 45° diagonal, it's column value C[k-1] will be one larger than C[k]. Similarly, if it is on the 135° diagonal, it's column value C[k-1] will be one smaller than C[k]. A conflicting queen two rows above will have C[k-1] values two larger or smaller than C[k-1], and so forth.

Figure showing this C[k] vector, {0,7,2,1,6,3,5,4} with k pointing to the C[5] element, which is a 3. The element 7 in C[1] is 4 larger than the 3 in C[5] and itis 4 places away from C[5] since 5-1 = 4. The element 1 is in C[3]. It is 2 smaller than the 3 in C[5] and it 2 away from C[5] since 5-3 = 2. These are conflicts; the rest of the elements below k do not conflict.

We can use this test for conflicts between the k-th queen and the earlier i-th queen:

if ((column[i] == column[k] - (k - i)) || (column[i] == column[k] + (k - i))) // conflict

This code returns one when the gloabal vector columns[] contains a solution or zero otherwise.

int queens(int k, int n) // N-queens test
	{ // n is the length of the vector, k is the position to begin testing
	if (k == n) return 1; // checking is complete - the solution has been found 
	for (int j = k; j < n; j++) // otherwise, permute and check the following queens
		{
		int temp = column[k]; column[k] = column[j]; column[j] = temp; // swap
		int conflicts = 0; // flag to keep track of conflicts
		 if (k != 0) for (int i = k-1; i >= 0; i--) // don't need to check when k == 0
			{
			counter++; // keep track of diagonal tests
			if ((column[i] == column[k] - (k - i)) || (column[i] == column[k] + (k - i))) // conflict
				{
				conflicts = 1;
				break; // no need to look further
				}
			}
			if (!conflicts && queens(k+1, n)) return 1; // solution found
		temp = column[k]; column[k] = column[j]; column[j] = temp; // not found, swap back
		}
	return 0; // no solution found
	} // end queens()

The attached script shows that this function produces the proper results. Notice that the number of comparisons is far fewer than N!.