[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes] 

cs2223, D97/98 Class 22

Random Numbers

We have already shown the use of the C/C++ random number generation function rand(). This algorithm is based on the algorithm in the ANSI C Standard.

// globalvariable
static unsigned long int next = 1;

int my_rand(void)
   {
   next = next * 1103515245 + 12345;
   return (unsigned int) (next / 65536) % 32768;
   }
   
void my_srand(unsigned int seed)
   {
   next = seed;
   }

As with all computer-based random number generators, this is actually a pseudo-random number generator. That means it cycles and repeats the same sequence of numbers over and over again. For most purposes, it is important that the cycle length be as long as possible. There is a macro RAND_MAX which tells the maximum number returned by the function rand(). According to the C standard, this number should be at least 32767, so we would expect a pseudo-random number generator to have a cycle length at least this long. If the length is less than RAND_MAX, there are some numbers the algorithm will not produce (for those familiar with discrete mathematics, this is a corollary of the pigenhole principle).

The attached script shows that rand() can have cycle lengths much less than RAND_MAX. The attached program which finds the minimum and maximum cycle lengths produced these results:

RAND_MAX = 32767
the seed 21939 produced the cycle length 0
the seed 978 produced the cycle length 359334

A better algorithm is one by S Park and K Miller, "Random number generators: Good ones are hard to find", Communications of the ACM, 10, 1988, pp1192-1201.

int my_rand(void)
	{
	next = next * 16807;
	return (unsigned int) next % 2147483647;
	}
	
void my_srand(unsigned int seed)
	{
	next = seed;
	}

This algorithm has longer repeat cycles and produces more uniformly distributed numbers. One problem is that this algorithm will not run properly on machines with small long ints. A version of this algorithm is given in MR Headington and DD Riley, 1997, Jones and Bartlett Publishers.

 int my_rand(void)
	{
	const long int multiplier = 16807;
	const long int maximum = 2147483647; // 2^31 - 1
	const long int quotient = 127773; // maximum / multiplier
	const long int remainder = 2836; // maximum % multiplier
	long int temp = multiplier * (next % quotient) - remainder * (next / quotient);
	next = (temp > 0) ? temp : temp + maximum;
	return (unsigned int) next;
	}
	
void my_srand(unsigned int seed)
	{
	next = seed;
	}

This algorithm breaks will run on computers with long ints as small as 4 bytes. For both of these forms of the function, the largest random number produced is 2147483646.

In all cases, it is important to "seed" the random number generator with a non-zero number which you are not likely to reuse frequently. If you seed with the same number, the function rand() will respond with the same sequence. That is useful for debugging but not for practical use. This command will seed the random number generator with the computer's clock time, which should not repeat with subsequent seedings.

		srand(time(NULL)); // use to seed random number generator

Be careful. If you use this command more frequently than you computer's clock ubdates (typically 1/sec to 60/sec), then you will obtain identical results as explained above. The usual practice is to seed once at the beginning of main().

Scaling the Random Numbers

The pseudo-random number generators produce values in the range 0 ->RAND_MAX. Other ranges are usually more convenient.

To produce a random number in the range 0->10, note that there are 11 values involved (max - min + 1 = 11) so we can use this command:

int the_number = rand() % (10 - 0 + 1);
int the_number = rand() % 11; // this one is better

To produce a random number in the range 3->9 (range = 9 - 3 + 1 = 7), use this command

int the_number = min + rand() % range;
int the_number = 3 + rand() % 7; // this one is better

This also works with negative numbers -9->-4 (range = 9 - 4 + 1 = 6), use this command

int the_number = -9 + rand() % 6;

Note, the modulus technique only works when the range is significantly less than RAND_MAX. If that is not the case, see below.

To produce a random float, use

float the_number = (float) rand() / (float) RAND_MAX;

This produces random numbers in the semi-open range 0<r<=1.0. Note, there are still only RAND_MAX possible floating points which can be generated by this approach. If you need more precision, see below.

To scale a floating point number to fit between a and b, use this command.

float a, b;
float the_number = a + (b - a) * (float) rand() / (float) RAND_MAX;

To increase the number of digits, you can generate the pseudo-random numbers digit by digit.

int places = 1, the_number = 0;
for (n = 1; n <= n_digits; n++)
	{
	the_number += places * (rand() % 10); // add a digit
	places *= 10; // the next goes one place to the left
	}

This same technique can be used for floating point numbers. But, remember that rand() still cycles and the cycle length is the number of digits which can be generated before they start repeating.

Integral of a function

Suppose you want to find the integral of a function, expressed as a C/C++ function.

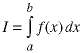
One not particularly good way to do this is by probabilistic programming, Assume the function is positive. Then make a rectangular box which encloses the function. Typically this means the left and right edges of the box are the limits of the integration and the height of the box is the maximum value of the function:

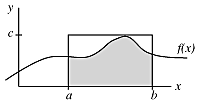
The area inside the box is just c(b-a) and the area under the cirve is just the integral we are looking for. Suppose we select points (x,y) inside the box. Some fraction will also fall in the shaded area. If we count the number which fall inside the shaded area, this gives us an estimate of the area under the curve, which is just the integral.

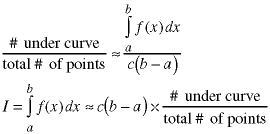
As a test, the attached script shows that the algorithm gives a reasonable approximation to the integral of the sine curve:

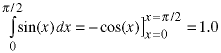
If the answer does not converge reasonably with large numbers of points, consider that the cause could be the cycle length of the random number generator. The solution is to use a better pseudo-random number generator.

[cs2223 text] [News] [Syllabus] [Classes]

Contents ©1994-1998, Norman Wittels
Updated 20Apr98