[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes] 

cs2223, D97/98 Class 20

Chained Matrix Multiplication

Matrix multiplication is an associative binary operation. That means that matrices are multiplied two at at time and the order in which a string of matrix multiplications is performed does not alter the result. We usually show this by means of parentheses:

A * (B * C) = (A * B) * C

Also, the number of matrix multiplications remains invariant - N matrices require N-1 matrix multiplications, no mater what order. What does change with the ordering of the matrix multiplications, however, is the number of individual matrix element multiplications required.

In multiplying two matrices, the number of columns in the first and the number of rows in the second must match - this means that matrix multiplication is generally not commutative (the order counts).

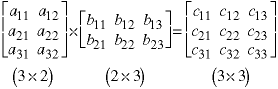
Figure showing that the multiplication of a (3x2) - 3 rows and 2 columns - matrix times a (2x3) matrix produces a (3x3) matrix.

The numbers in parentheses are the orders of the respective matrices - the number of rows and columns, respectively. The value of each of the elements in the product is formed by the sum of individual products - the number of which is equal to the common number of columns in the first or rows in the second.

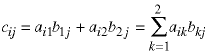
c(ij) = a(i1) * b(1j) + a(12) * b(2j) = sum(k=1 -> 2; a(ik) * b(kj))

And, since there are three possible values of i and three possible values of j, the number of multiplications of matrix elements is.

3 * 2 * 3 = 18

In general, multiplying a(i x k)matrix by a(k x j)matrix, requires i * k * jindividual multiplications.

The order in which we mutiply the matrices in a chain of matrix multiplications can greatly influence the number of multiplications which are required. An an example, let's multiply these five matrices:

M = A * B * C * D * E

matrix

order

 A

 (100 x 1)

 B

 (1 x 99)

 C

 (99 x 1)

 D

 (1 x 85)

 E

 (85 x 1)

If we consider two ways of splitting up the multiplications, we get two very different numbers of element multiplications:

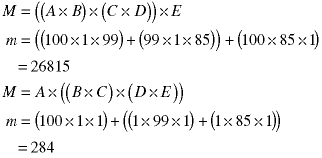
M = ((AB) * (CD)) * E; m = ((100*1*99) + (99*1*85)) + (100*85*1) = 26815; M = A * ((BC) * (DE)); m = (100*1*1) * ((1*99*1) + (1*85*1)) = 284

Optimal Matrix Multiplication

We want to find the multiplication order which optimizes matrix multiplication - the one which requires the fewest number of binary matrix elements multiplication. To get an idea how this works, look at the number of ways to do the final multiplication: We use the notation mij to denote the optimal number of multiplications of the subsequence of matrices from i to j: And let the vector dk denote the dimensions of the matrices in the list - which will be one more than the number of matrices. In our example, here is the d vector.

d = {100,1,99,1,85,1}

Then there are four possible ways to do the last multiplication and there are four corresponding values for the optimal number of element multiplications:

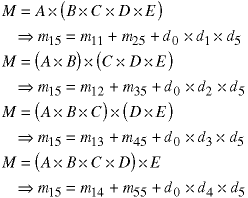
M = A * (B*C*D*E) -> m15 = m11 = m25 = d0 * d1 * d5; M = (A*B) * (C*D*E) -> m15 = m12 + m35 = d0 + d2 + d5; M = (A*B*C) * (D*E) -> m15 = m13 + m45 + d0 + d3 + d5; M = (A*B*C*D) * E -> m15 = m14 + m55 + d0 + d4 + d5

Since we want the optimal value for m15, we need to take the minimum of the above for values. And, of course, we need to find the optimimum way to place the parentheses in each of the two sub-sequences to calculate the restof the values which are combined to find m15. This problem has two of the elements of dynamic programming: a cost function which is calculated recursively (to avoid having to recalculate intermediate values) and a way to conbine optimal sub-solutions to form an optimal solution. The only thing missing is a way to work backwards from the optimal value of m15 and determine which parantheses placement produced the optimal value. We cannot do it from the optimal value alone. The above case shows there is one of four possible routes which led to the optimal solution. In a problem with N matrices,there are N-1 possible last steps. So, we will use two matrices - one to keep track of the optimal values as we calculate them recursively, and one to keep track of which path led to the optimal solution.

Solution Matrices

The above solution for m15 can be generalized to calculate mij, the optimal number of element multiplications necessary to multiply the subsequence of matrices i through j.

m(i,j) = min{m(i,i+k) + m(i+k+1,j) + d[i-1]*d[i+k]*d[j]}

The intermediate value k can take on all values between 0 andj-i-1. If we plug the values

i=1, j=5; k = 0 -> (j-i-1) = 0 -> 3

into the above equation, we get the four expressions for the last multiplication in our example:

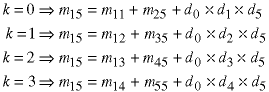
k=0 -> m15 = m11 + m25 + d0*d1*d5; k=1 -> m15 = m12 + m35 + d0*d2*d5; k=2 -> m15 = m13 + m45 + d0*d3*d5; k=3 -> m15 = m14 + m55 + d0*d4*d5

We cannot calculate these four expressions to find the minimum without knowing the other values of mij. We find those values recursively and fill in our m matrix:

Figure showing the m matrix. The main diagonal elements m11, m22, ... , m55 all correspond to sequences of length 1. The next diagonal up has the elements m12, m23, m34, and m45, all corresponding to sequences of length 2. The next diagonal up has elements m13, m24, m35, and so forth. The last diagonal (top right element in the matrix) is m15. All elements below the diagonal are left blank because their values will never be used.

We've left off everything below the main diagonal because a subsequence cannot start before it begins! Note, also, that we have explicitly shown how subsequences of the same length all lie on the same diagonal because the length is justj-1+1.

Length = 1 and 2

Now we fill in the matrix, recursively. The subsequences of length one (main diagonal) all have value zero. No multiplication is involved in dealing with a subsequence of length one (all the magic happens in producing the other subsequence and in the multiplication of the two subsequences).

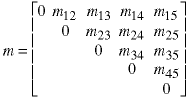
Figure showing the m matrix with all elements on the main diagonal - the ones corresponding to sequences of length one - set to zero.

The coefficients of length 2 all involve just the d vector values.

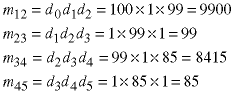
m12 = d0*d1*d2 = 100*1*99 = 9900; m23 = d1*d2*d3 = 1*99*1 = 99; m34 = d2*d3*d4 = 99*1*85 = 8415; m45 = d3*d4*d5 = 1*85*1 = 85

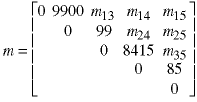
Figure showing the matrix with the second diagonal - the one corresponding to sequences of length 2 - replaced by the values calculated above.

Now we use the recursive equation above to find the rest of the values, one length at a time.

Length = 3

These calculations will all use k values between 0 and 1:

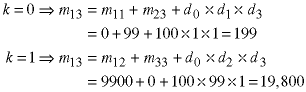
k=0 -> m13 = m11 = m23 + d0*d1*d3 = 0 + 99 + 100*1*1 = 199; k=1 -> m13 = m12 + m33 + d0*d2*d3 = 9900 + 0 + 100*99*1 = 19,800

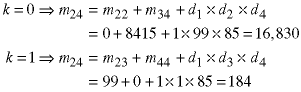
k=0 -> m24 = m22 +m34 + d1*d2*d4 = 0 + 8415 + 1*99*85 = 16,830; k=1 -> m24 = m23 + m44 + d1+d3+d4 = 99 + 0 + 1*1*85 = 184

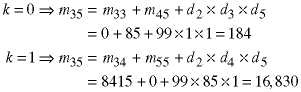
k=0 -> m35 = m33 + m45 + d2*d3*d5 = 0 + 85 + 99*1*1 = 184; k=1 -> m35 = m34 + m55 + d2*d4*d5 = 8415 + 0 + 99*85*1 = 16,830

The optimal values (minima) are:

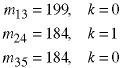
m13 = 199, k=0; m24 = 184, k=1; m35 = 184, k=0

The first equation means that the optimal way to do the multiplication of the first three matrices is

A * (B*C)

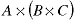
and 199 is the number of element multiplications required. The value k=0 is what tells us to put the interior parentheses after matrix A since matrix is the first matrix in the subsequence and k+1 = 1. Similarly, the other two results tell us the best way to do the other two submatrices of length 3 are:

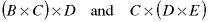
(B*C) * D and C * (D*E)

As we stated above, we need to keep track of how we got the minimum so let's form a k matrix, too:

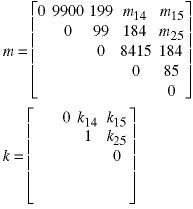
Figure showing the m matrix with the three values calculated above entered along the diagonal which represents sequences of length three. A k matrix - also 5x5 - is shown in which the corresponding diagonal contains the values 0,1,0. All elements below this are empty because their values don't matter.

We only need to use the k values for lengths 2 and above, so even more of it is left blank.

Length = 4

These calculations will use k values between 0 and 2:

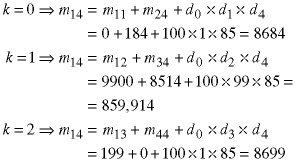
k=0 -> m14 = m11 + m24 + d0*d1*d4 = 0 + 184 + 100*1*85 = 8684; k=1 -> m14 = m12 + m34 + d0*d2*d4 = 9900 + 8514 + 100*99*85 = 859,914; k=2 -> m14 = m13 + m44 + d0*d3*d4 = 199 + 0 + 100*1*85 = 8699

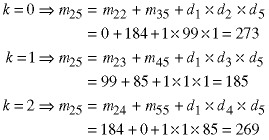
k=0 -> m25 = m22 +m35 + d1*d2*d5 = 0 + 184 + 1*99*1 = 273; k=1 -> m25 = m23 + m45 + d1*d3*d5 = 99 + 85 + 1*1*1 = 185; k=2 -> m25 = m24 + m55 + d1*d4*d5 = 184 + 0 + 1*1*85 = 269

The optimal values (minima) are:

m14 = 8685, k=0; m25 = 185, k=1

These correspend, respectively, to the subsequences of length 4:

A*(BCD), (AB) * (CD)

Put these values into the m and k matrices:

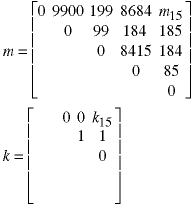
These new m values have been added to the m matrix along the diagonal corresponding to subsequences of length 4 and the values 0,1 are placed int he corresponding diagonal in the k matrix.

Length = 5

This calculations will use k values between 0 and 3: The equations were given above so we only have to put in the values, which have now been calculated:

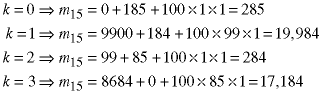
k=0 -> m15 = 0 + 185 + 100*1*1 = 285; k=1 -> m15 = 9900 + 184 + 100*99*1 = 19,985; k=2 -> m15 = 99 + 85 + 100*1*1 = 284; k=3 -> m15 = 8684 + 0 + 100*85*1 = 17,184

The optimal value (minima) is:

m15 = 284, k=2

The final matrices are:

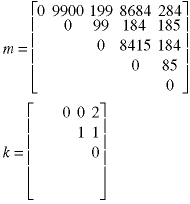
The values 284 and 2 have been placed in the top right elements of the m and k matrices, respectively.

This tells us that a solution to multiplying the five matrices can be found which involves 284 multiplications of matrix elements. The k=2 tells us that the first set of internal parentheses come after the first matrix:

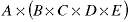
A*(BCDE)

Next the subsequences are recursively parsed into their subsequences using the same matrices. The first subsequence corresponds to m11 and m25. The first one cannot be subdivided any further (that is what the m11=0 is telling us). The m25 has k=1, which tells us that the next set of internal parentheses goes after matrix 3:

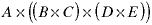
A * ((BC) * (DE))

The next parsing is of m23, but the fact that there is no entry in the k matrix tells us that we need go no further.--------------------
[WPI Home Page] [cs2223 home page]  [cs2223 text] [News] [Syllabus] [Classes] 

Contents ©1994-1998, Norman Wittels
Updated 15Apr98