cs2223 Class 9

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 9

Heaps

A heap is a binary tree with three key properties.

It is a "mostly complete" or "essentially complete" binary tree
All nodes are moved as far up and left as possible
Every node has a value greater than or equal to the values of its children

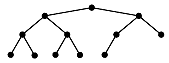
Here is a diagram of a heap.

Figure showing a binary tree with the above properties

The first heap property means than each node can have one leaf, two leaves, or two branches, but not one branch or one branch and one leaf. In English, the first two conditions mean that all leaves are confined to the left side of the bottom level - level 0 - of the tree or the right side of the next level up - level 1. If we add nodes to a heap, we fill from left to right in the bottom level of the tree.

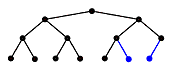
Figure showing two more leaves added to the bottom of the tree, as described

The third property of the heap allows for duplicate values, but children can never have greater values than their parents.

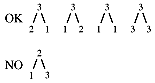
Examples showing that all cases are valid except when a child has a value greater than its parent

Unlike the binary search tree, in the heap, the value of the left child can by greater than, less than, or equal to the value of the right child. Number the nodes in rows.

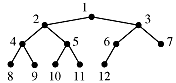
Figure of binary tree with node numbers increasing from left to right in rows; the root is node 1 and the right-most node in the bottom row has value 12

Note that the numbering is 1->12 not 0->11. Then it is easy to match parents and children using the indices of the notes.

parent(node (i)) = node(i/2)

left_child(node(i)) = node(2i)

right_child(node(i)) = node(2i+1)

These relationships assume integer mathematics.

Note also that in a heap with n nodes, n/2 is the last node which has children.

The heap conditions make it easy to store heaps in arrays. If a heap has been stored as a tree using linked lists or other technologies, it can be stured in an array using a queueing process. This same process is also used for printing trees.

Begin at the root, node n = 1, and recursively:

Put the index of the n-th node's left child (if there is one) into the queue

Put the index of the n-th node's right child (if there is one) into the queue

Print the value of n-th node, or print it

Dequeue the top value in the queue and call it n. Stop if the queue is empty.

Operations on Heaps

We discussed operations performed on heaps. Note that most of them use the heap properties to simplify the algorithms.

Percolation

Suppose a value in a node is increased. The change can have no effect on the node's children but it can destroy the heap relationship with the node's parent. Recursively swap the node's value with it's parent's until the heap relationship is restored. The upward recursion stops whenever the parent's value is not smaller at the tree's root (n/2 < 1).

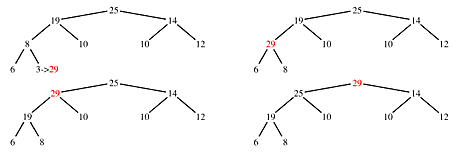
A set of figures showing a high value percolating upward from a leaf to become the root through a sequence of child/parent swaps

Becuase the height of the tree is the floor (lowest integral value) of lgn, percolation is of order O(lgn).

Sifting

Suppose a value in a node is decreased. The change can have no effect on the node's parent but it can destroy the heap relationship with the node's children. Recursively swap the node's value with the largest of it's children until the heap relationship is restored. The downward recursion stops whenever neither child's value is smaller or whenever the bottom of the tree is reached (2n > size or 2n+1 > size).

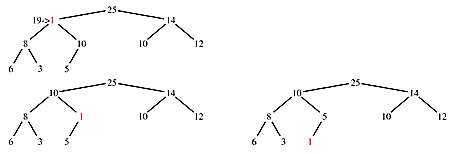
Figures showing a low value sifting downward to a leaf in the bottom row through a sequence of parent/child swaps

Becuase the height of the tree is the floor (lowest integral value) of lgn, sifting is of order O(lgn).

Insertion

To insert a value into a heap, put it into the first open space in the heap, which is at the end of the array (n = size+1). Since this value could be greater than it's parent, use percolation to restore the heap propery. The actual insertion step is of order O(1) so the order of the insertion algorithm is the same as the order of percolation, O(lgn). Filling a heap by sequentially inserting values is of order O(nlgn).

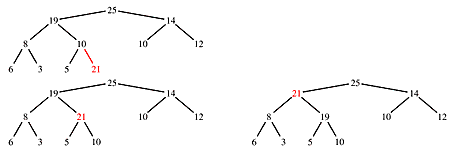
Images showing a new value being inserted in the first available leaf in the bottom row then percolating upward to its correct position

Deletion

To deleta a value from a heap, swap it with the last value in the heap (n = size+1) and reduce the heap size by one. Since the swap almost certainly destroys the heap property, restore it using sifting or percolation, depending on the value swapped into the node. Since performing both percolation and sifting at the node costs only one more comparison than doing only the "correct" operation, it is usuall to write the deletion algorithm so it does both after the swap. The order of deletion is the same as the order of percolation and sifting, O(lgn). Don't forget the special case when the last element is the one being deleted!

Build or Restore a Heap

The easiest way to turn an array into a heap is just to restore the heap conditions in the array. This can be done by starting at the bottom and sequentially sifting each element in the array. Sifting is not done at leaves so the process can begin at the element n/2, where n is the array size. Restoration is of order is of order O(nlgn).

Sort a Heap

Heaps are easy to build and maintain, but itis hard to find specific values in the heap. For example, the maximum value is always at the root, but the minimum value can be in any leaf, which is a problem because a heap of size n has about n/2 leaves! The heapsort algorithm rearranges the heap arary to put the values in increasing sequential order - the smallest is in the first place. This heapsort algorithm is used recursively.

Swap the root, the largest value in the array, with the last (smaller) element in the array.

Freeze the largest value in it's new place at the end of the array (don't allow it to change)

Sift the heap beginning at the root to restore the heap properties. Ignore frozen values

Stop when only two values are unfrozen.

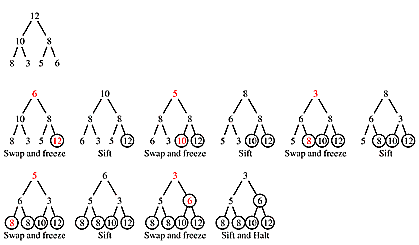
Sequence of images illustrating the algorithm described above

To make the array back into a heap, just sort it again. This works because the second sort results in an array with decreasing values and such an array is always a heap (because decreasing orders assures that each node has a greater value than any of its children, which come later in the array). The heapsort algorithm is of order O(nlgn).