cs2223 Class 3

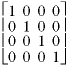
[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 3

Measuring Calculation Time

One way to measure the complexity of a calculation is ty measuring the execution time. We demonstrated the Timer class. When an instance of a Timer is instantiated, the creation time is noted. When the instance is deleted, the time difference is computed and printed. The source code is contained in the CCC directories:

/cs/cs2223/classes/class03/Timer/
/cs/cs2223/util/Timer/

The class03 directory also contains the program test.C, which demonstrates operation of the Timer class. The attached script demonstrates operation of the test program.

There are two major limitations with using execution "time" as an indicator of computational complexity. First, the time required depends on what else the computer is doing. In a multi-tasking environment (many jobs runing at the same time), timing measurments are subject to error. Second, the precision of the measurement is low. The precision is limited by the clock update rare - typically one to sixty times per second. A lot of computer operations can be performed in those intervals, so the measured results are not precise.

Note that the header file Timer.h also includes the generic header file headers.h. Including the complete set of available header files slightly increases the compilation time but has no impact on object file size or program execution time - assuming the compiler is moderately intelligent. A copy of headers.h is in the CCC directory:

/cs/cs2223/util/

Counting Operations

Another way to measure computational complexity is to count the number of times the command of interest is executed. One way to do this is to create a global (external) variable which hold the count of command executions. This count is incremented as required and its final value is printed out at the end of the computation.

We demonstrated the program minval.C. This program is based on the algorithm for finding the minimum value in an array, shown in Class 1. We expect the number of additions to be identical to the array size, and the attached script shows this is true. The source code for minval.C is contained in the CCC directory:

/cs/cs2223/classes/class03/

There are several interesting features in minval.C. First, note how the defult response to a memory allocation error - program abort - has been replaced by a call to the function, new_error_handler(), which gracefully reports the error. The methods in the ANSI draft C++ standard for handling exceptions, of which this is an example, are still not fully implemented in most C++ compilers. This is discussed more fully in the Class 19 notes in the cs2005 website.

The function shuffle() shows one way to randomize an array. Each element in the array is sequentially swapped with another element selected at random. The index of the "random" element is found using rand() % nmax, where nmax is the size of the array. This technique works for small values of nmax, but as nmax approaches RAND_MAX - the size of the largest random number generataed by the function rand() - the numbers produced this way are insufficiently "random". On most systems, RAND_MAX is around 32767.

Index Matrices

We looked at an algorithm which generates an index matrix - a matrix with all elements zero except the diagonal elements which are all one. Here is an index matrix of order 4:

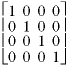
4x4 identity matrix

The algorithm comprises two nested loops:

		for (int y = 0; y < n; y++)
			for (int x = 0; x < n; x++)
				{
				if (x == y) *(array + n * y + x) = 1;
				else *(array + n * y + x) = 0;

}

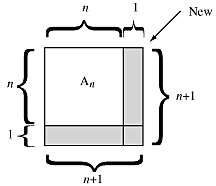
How many times are array values replaced? Since each loop independently counts to n, we expect the number of replacements to equal n². We developed the recurrence relation for A_n, the number of replacements in a square matrix of order n. When n is increased by one, the number of new elements added to the array, which equals the additional number of replacements, is

figure showing that adding one row and column increases the number of elements by 2n + 1 so

Substituting n-1 for n, we obtain the usual form of the recurrence relation:

Later we will study how to solve equations of this form, but we can prove that our guess is correct by direct substitution:

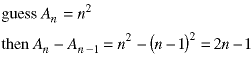
guess: A(n) = n^2;
then A(n) = A(n-1) = n^2 - (n - 1)^2 = 2n -1

Since both sides of the last equation are the same, our guess was correct. This is a loose form of a proof by induction, which we will study later.

The program identity.C demonstrates that the answer is correct. It creates identity matrices of order 1, 10, ... and counts the number of replacements, as shown in the attached script. The source code for identity.C is contained in the CCC directory:

/cs/cs2223/classes/class03/