cs2223 Class 2

[WPI] [cs2223] [cs2223 text] [News] [Syllabus] [Classes]

cs2223, D97/98 Class 2

Recurrence Relation

Look again at the minimum int algorithm shown in Class 1. We can describe the number of additions required for an array of length n by using the symbol A_n. Yesterday we showed that this can be written as:

For this algorithm, we can calculate the number of additions easily, for any value of n. Often, however, that is a difficult task. It is usually easier to calculate the increase in the number of additions when the array size is increased by one. Since one more time through the loop adds one more addition, we can write:

This equation is valid for all positive values of n, so we can write it in its more usual form:

This is called a recurrence relation or a recurrence or a difference equation. It is closely related to the differential equations of continuous variables. The change in the value of n is one so we can divide both sides by that change in n:

The equivalent differential equation is:

It has the solution

We cannot use differential calculus to solve our recurrence relation because the limit does not exist because A_n is not a continuous function - it only exists at integral values on n. However, using techniques we will discuss later, we can show that its solution is:

The first term on the right is the initial condition. In our case, it is zero since there are no additions (inrements) performed when n is zero.

N-digit addition

Consider how numbers are added using decimal notation - lowest to highest-order digits plus a carry digit of 0 or 1:

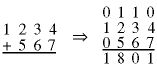
sum of 1234 + 567 is 1801

If the length of the longest number is n digits, the number of additions is 2n. (recall that addition is a binary operation - only two digits can be added at a time). We expect that the recurrence relation and solution for the number of additions will be:

We discussed how to write an algorithm to implement this algorithm, including file formats, order of reading and adding digits, etc. We designed and demonstrated an algorithm based on using stacks to store the numbers. The source code and data files are in the CCC directory: /cs/cs2223/classes/class02 and a script file showing the program running is attached.