
Quadric surfaces are defined by quadratic equations in two dimensional space. Spheres and cones are examples of quadrics. The quadric surfaces of RenderMan are surfaces of revolution in which a finite curve in two dimensions is swept in three dimensional space about one axis to create a surface. A circle centered at the origin forms a sphere. If the circle is not centered at the origin, the circle sweeps out a torus. A line segment with one end lying on the axis of rotation forms a cone. A line segment parallel to the axis of rotation forms a cylinder. The generalization of a line segment creates a hyperboloid by rotating an arbitrary line segment in three dimensional space about the Z axis. The axis of rotation is always the z axis. Each quadric routine has a sweep parameter, specifying the angular extent to which the quadric is swept about z axis. Sweeping a quadric by less than 360 degrees leaves an open surface.
Many common shapes can be modeled with quadrics. Although it is possible to convert quadrics to patches, they are defined as primitives because special-purpose rendering programs render them directly and because their surface parameters are not necessarily preserved if they are converted to patches. Quadric primitives are particularly useful in solid and molecular modeling applications.
All the following quadrics are rotationally symmetric about the z axis. In all the quadrics u and v are assumed to run from 0 to 1. These primitives all define a bounded region on a quadric surface. It is not possible to define infinite quadrics. Note that each quadric is defined relative to the origin of the object coordinate system. To position them at another point or with their symmetry axis in another direction requires the use a modeling transformation. The geometric normal to the surface points ``outward'' from the z-axis, if the current orientation matches the orientation of the current transformation and "inward" if they don't match. The sense of a quadric can be reversed by giving negative parameters. For example, giving a negative thetamax parameter in any of the following definitions will turn the quadric inside-out.
Each quadric has a parameterlist. This is a list of token-array pairs where each token is one of the standard geometric primitive variables or a variable which has been defined with RiDeclare. Position variables should not be given with quadrics. All angular arguments to these functions are given in degrees. The trigonometric functions used in their definitions are assumed to also accept angles in degrees.
RiSphere( radius, zmin, zmax, thetamax, parameterlist ) RtFloat radius; RtFloat zmin, zmax; RtFloat thetamax;
Requests a sphere defined by the following equations:

Note that if zmin > -radius or zmax < radius, the bottom or top of the sphere is open, and that if thetamax is not equal to 360 degrees, the sides are also open.
RIB BINDING Sphere radius zmin zmax thetamax parameterlist Sphere [radius zmin zmax thetamax] parameterlist EXAMPLE RiSphere(0.5, 0.0, 0.5, 360.0, RI_NULL);
RiCone( height, radius, thetamax, parameterlist ) RtFloat height; RtFloat radius; RtFloat thetamax;
Requests a cone defined by the following equations:
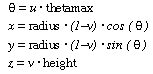
Note that the bottom of the cone is open, and if thetamax is not equal to 360 degrees, the sides are open.
RIB BINDING
Cone height radius thetamax parameterlist
Cone [height radius thetamax] parameterlist
EXAMPLE
RtColor four_colors[4];
RiCone(0.5, 0.5, 270.0, "Cs", (RtPointer)four_colors, RI_NULL);
RiCylinder( radius, zmin, zmax, thetamax, parameterlist ) RtFloat radius; RtFloat zmin, zmax; RtFloat thetamax;
Requests a cylinder defined by the following equations:
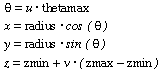
Note that the cylinder is open at the top and bottom, and if thetamax is not equal to 360 degrees, the sides also are open.
RIB BINDING Cylinder radius zmin zmax thetamax parameterlist Cylinder [radius zmin zmax thetamax] parameterlist EXAMPLE Cylinder .5 .2 1 360
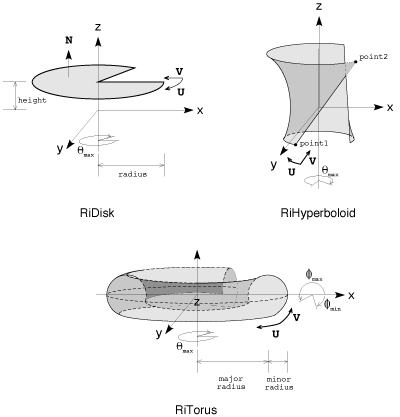
RiHyperboloid( point1, point2, thetamax, parameterlist ) RtPoint point1, point2; RtFloat thetamax;
Requests a hyperboloid defined by the following equations:
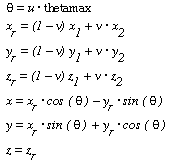
assuming that point1 = (x1,y1, z1) and point2 = (x2, y2, z2).
The cone, disk and cylinder are special cases of this surface. Note that the top and bottom of the hyperboloid are open when point1 and point2, respectively, are not on the z-axis. Also, if thetamax is not equal to 360 degrees, the sides are open.
RIB BINDING Hyperboloid x1 y1 z1 x2 y2 z2 thetamax parameterlist Hyperboloid [x1 y1 z1 x2 y2 z2 thetamax] parameterlist EXAMPLE Hyperboloid 0 0 0 .5 0 0 270 "Cs" [1 1 1 .5 .9 1 .2 .9 0 .5 .2 0]
RiParaboloid( rmax, zmin, zmax, thetamax, parameterlist ) RtFloat rmax; RtFloat zmin, zmax; RtFloat thetamax;
Requests a paraboloid defined by the following equations:
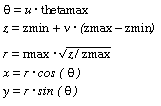
Note that the top of the paraboloid is open, and if thetamax is not equal to 360 degrees, the sides are also open.
RIB BINDING Paraboloid rmax zmin zmax thetamax parameterlist Paraboloid [rmax zmin zmax thetamax] parameterlist EXAMPLE Paraboloid .5 .2 .7 270
RiDisk( height, radius, thetamax, parameterlist ) RtFloat height RtFloat radius; RtFloat thetamax;
Requests a disk defined by the following equations:
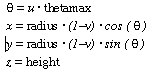
Note that the surface normal of the disk points in the positive z direction when thetamax is positive.
RIB BINDING Disk height radius thetamax parameterlist Disk [height radius thetamax] parameterlist EXAMPLE RiDisk(1.0, 0.5, 270.0, RI_NULL);
RiTorus( majorradius, minorradius, phimin, phimax, thetamax, parameterlist ) RtFloat majorradius, minorradius; RtFloat phimin, phimax; RtFloat thetamax;
Requests a torus defined by the following equations:

Note that if phimax-phimin or thetamax is not equal to 360 degrees, the torus is open.
RIB BINDING
Torus rmajor rminor phimin phimax thetamax parameterlist
Torus [rmajor rminor phimin phimax thetamax] parameterlist
EXAMPLE
Torus 1 .3 60 90 360
Quadric surface primitives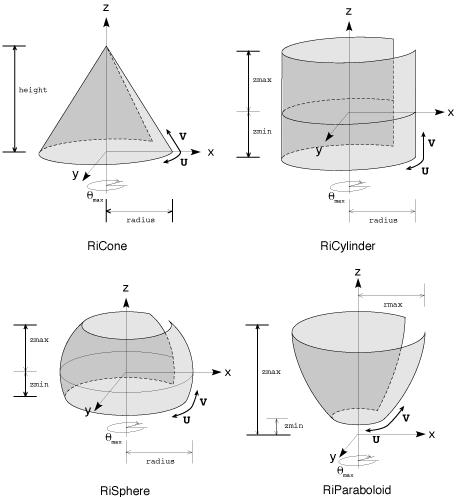
Copyright - Sudhir R Kaushik (sudhir@cs.wpi.edu)