Overview of Acceleration Techniques

Ray tracing acceleration techniques can be can be placed into three categories:

Ones that reduce the average time needed to intersect a ray with the world
Ones that reduce the total number of rays that need to intersect with the world
Ones that replace the individual rays with with a more generalized entity

Techniques that reduce the total number of rays that intersect with the world are often used in conjunction with anti-aliasing techniques which cast multiple rays for each pixel. The reader is directed to [1] for an introduction to Adaptive Super-sampling, Stochastic Ray Tracing, and Statistical Super-sampling as these techniques are beyond the scope of this presentation.

Techniques that reduce the average time needed to intersect a ray with the world can then be divided into 2 sub-categories.

Faster object intersection algorithms
Fewer object intersections

Faster Object Intersection Algorithms

These algorithms aim at reducing the average cost of testing a ray for intersection with an object. The predominant feature in these algorithms is to order the calculations in a way that allows intermediate tests for intersection to be performed. The tests, based on the current stage of calculation, are able to determine if the ray misses the object. If it does no further calculations are needed. Eric Haines in [1] offers a geometric solution to intersection with a sphere which has four stages of calculation.

Find if the ray's origin is outside the sphere.
Find the closest approach, t_ca, of the ray with the sphere
- If the ray is outside and points away from the sphere, the ray must miss the sphere.
Find the squared distance from the closest approach, t_2hc, to the sphere surface.
- If the value is negative the ray misses
Using t_ca & t_2hc calculate the time, t, of intersection with the sphere
- t = t_ca - sqrt(t_2hc), origin outside sphere
- t = t_ca + sqrt(t_2hc), origin inside sphere

Fewer Object Intersections

The goal of these techniques is to reduce the number of object intersection tests for a given ray. These can be broken down into categories as follows.

Bounding Volumes
Spatial Subdivision
- Nonuniform
- Uniform
Directional Techniques
- Light Buffer
- Ray Coherence
- Ray Classification

The following is meant as a summary of the above techniques as presented by James Arvo and David Kirk in [1]. All images are based on those from [1]

Bounding Volumes

Instead of each ray against every ray test the ray against collection of objects which are known to be contained within a bounding volume. If the ray does not hit the bounding volume it cannot hit any of the objects within. This method lends itself to hierarchical collections in which the objects within a bounding volume can themselves be bounding volumes containing ...

Issues: Tightness of Fit vs. Speed of Intersection

Ideally one wants to have a bounding volume that is a tight fit to the collection of objects within. However, this can often require complex shapes whose intersection cost rivals that if the objects were considered individually

Bounding volumes and there effectiveness will be discussed further in the implementation section

3-D Spatial Subdivision

Non-Uniform & Uniform

Non-Uniform Subdivision

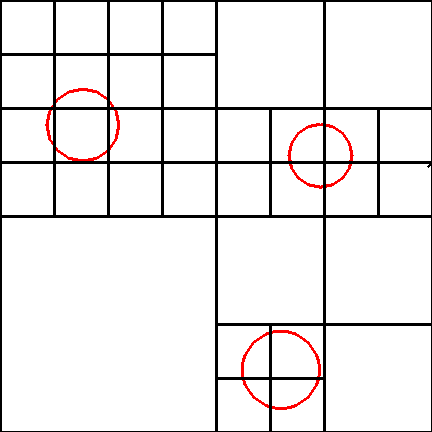
In Non-Uniform subdivision the world is divided into 8 quadrants, a check is then made of the number of objects whose surfaces occupy some portion each quadrant. If the number is greater then some threshold that quadrant is further subdivided into eight quadrants, etc.. An octree is used as the data structure for indexing the candidate objects for each voxel in a hashtable. Tracing a ray involves finding which voxel the ray originates from, checking it against all the objects in that voxels candidate list for intersection, if no objects are hit, determine which voxel the ray passes through next (How?) and repeat the process.

Uniform Subdivision

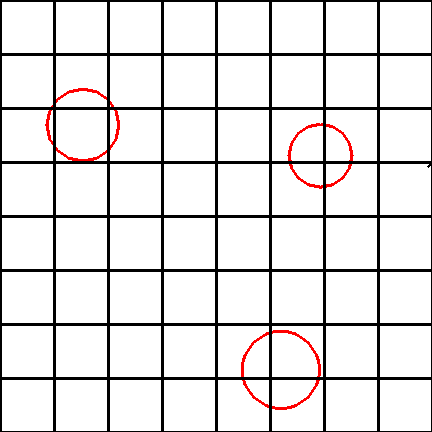
Uniform subdivision is very much the same except the world is divided into equal sized voxels Because of this algorithms similar to the Bresenham line drawing algorithm can be used for quickly determining which voxel the ray hits next.

Issues:

The same ray may test the same object for intersection multible times. Mailbox?
Need to make sure the intersection occurs in that voxel

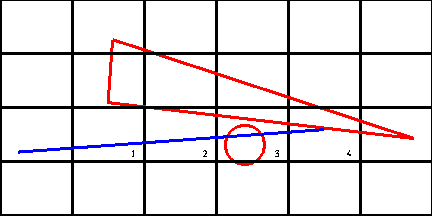
Both of these issues are illustrated above. The triangle will be tested for intersection with the ray in voxel 2. If a check is not made to see that the intersection occurs in that voxel the correct intersection with the sphere will not be found. When the ray enters voxel 3 the intersection for the triangle should not have to be recalculated. When ever a ray is intersected with an object the result of that intersection along with the rays ID is stored in the objects mailbox. When a object is tested for intersection with a ray the ray's ID is first tested against the ID in the mailbox. If they match the result stored in the mailbox can be used avoiding the recalculation.

Directional Techniques

The Directional Cube

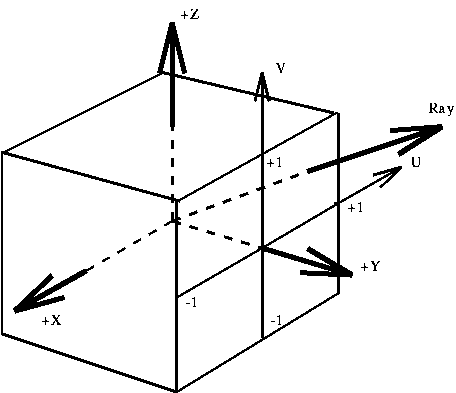
A directional cube is an axis aligned cube with side of length 2 at the origin. The six faces are labeled by there dominant axis +X, -X, +Y, -Y, +Z, -Z. A ray can be represented as two coordinates (u, v) on one of these faces. Also the surface of each of the faces can subdivided (uniform or non-uniform) to define directional pyramids with the origin at there apex

The Light Buffer

The light buffer is used as a preprocessing step to ray tracing to speed-up the calculation of shadows. It uses a directional cube centered at the light source and surface sub-division (of the directional cube). Each Object in the world is then projected onto each face of the cube. Candidate lists for each region can be formed. During ray tracing all that is needed is to determine which region in which surface the ray passes through, and check it against the candidate list for that region.

Ray Coherence

Same idea as the light buffer applied to every object in the world. For non-shadowing rays need to find the closest intersection not just any.

Ray Classification

In three space rays have five degrees of freedom corresponding to the points R3 x S2 where S2 is the unit sphere in three space. The algorithm partitions the 5-D space into regions encoded as 5-D hypercubes and associating a complete list of candidate objects with each. A hypercube represents a collection of rays with similar origins and directions. To intersect a ray locate the hypercube that contains the 5-D equivalent of the ray and test only those objects in the associated candidate list.

The above presentation is by no means complete. Its purpose was to demonstrate that there are a variety of techniques available for improving ray tracer performance. The potential benefit of implementing any technique should be weighed against the requirements of the system and the effort needed both in implementation and maintenance of a more complex system.