Particle Systems
by Allen Martin
Introduction
The term particle system is loosely defined in computer
graphics. It has been used to describe modeling techniques, rendering
techniques, and even types of animation. In fact, the definition of a
particle system seems to depend on the application that it is being
used for. The criteria that hold true for all particle systems are
the following:
Collection of
particles - A particle system is composed of one or more
individual particles. Each of these particles has attributes that
directly or indirectly effect the behavior of the particle or
ultimately how and where the particle is rendered. Often, particles
are graphical primitives such as points or lines, but they are not
limited to this. Particle systems have also been used to represent
complex group dynamics such as flocking birds.
Stochastically
defined attributes - The other common characteristic of all
particle systems is the introduction of some type of random element.
This random element can be used to control the particle attributes
such as position, velocity and color. Usually the random element is
controlled by some type of predefined stochastic limits, such as
bounds, variance, or type of distribution.
This summary will present three different particle systems, two of
which were created by Reeves [REE83] [REE85] and one created by
Reynolds [REY87]. In addition, images from some example particle
systems based on Reeves initial model [REE83] will be presented.
Using Particle Systems to Model Fire and Explosions
Reeves initially used the term "particle system" to describe a method
he used to create a sequence of images for the move Star Trek II:
The Wrath of Khan. The effect he was trying to create was that of
a bomb exploding on the surface of a planet and fire spreading out
from the point of impact to eventually engulf the planet. Each
particle in this system was a single point in space. The fire was
represented by thousands of these individual points. Typical
polygonal rendering methods create objects with straight edges, but
representing the fire by thousands of points gives the fire a "fuzzy"
shape. Reeves calls an object made up of particles a fuzzy
object.
Each object in Reeves particle system had the following attributes:
Position
Velocity (speed
and direction)
Color
Lifetime
Age
Shape
Size
Transparency
Particle Life Cycle
Each particle goes through three distinct phases in the particle
system: generation, dynamics, and death. These phases are described
in more detail here:
Rendering
When rendering this system of thousands of particles, some assumptions
have to be made to simplify the process. First, each particle is
rendered to a small graphical primitive (blob). Particles that map to
the same pixels in the image are additive - the color of a pixel is
simply the sum of the color values of all the particles that map to
it. Because of this assumption, no hidden surface algorithms are
needed to render the image, the particles are simply rendered in
order. Effects like temporal ant-aliasing (motion blur) are made
simple by the particle system process. The position and velocity are
known for each particle. By rendering a particle as a streak, motion
blur can be achieved.
Using Particle Systems to Model Trees
Reeves used the particle system approach to model trees in the
animated short movie The Adventures of Andre and Wally B.
[REE85] Each tree was created by using a particle system, and the
position of the trees within the forest was also controlled by a
particle system. The major enhancement over the previously mentioned
particle system is the rendering algorithm used. In The Adventures
of Andre and Wally B. a more traditional rendering method is used,
and the previous simplification of rendering the particles in order
and making them additive is not used. In addition, the generation
shape of the particle system is not fixed, but is dependent on the
current state. For example, leaves may only be created near the ends
of branches.
Tree Particle System Rendering Technique
The particles of the trees are small circles used to represent leaves
and lines used to represent branches. A more traditional rendering
technique is used that is based on the painter's algorithm. Because
of the large number of particles, standard lighting and shadow
calculations are computationally prohibitive, so more reasonable
solutions must be made.
Self
Shadowing - Particles on the outside of the tree are more likely
to be directly illuminated then points on the inside of the tree due
to the self shadowing of the tree. To model this, a lighting model is
used where a cone is used as the bounding volume for the tree. The
distance from the point to the outside of the bounding volume along
the line between the point and the light source is used as a parameter
to the lighting equation. The lighting equation has a maximum value
at the outer edge of the bounding volume facing the light, and
decreases exponentially inside the tree. The previously mentioned
distance parameter is used as the exponent in this equation.
Ambient
Lighting - Ambient lighting is based on an equation similar to the
self shadowing equation. Since ambient light is not based on direct
illumination from a light source the distance metric is made from the
point being illuminated horizontally out to the edge of the bounding
volume.
External
Shadowing - In addition to shadows cast by the tree on itself,
shadows cast from neighboring trees must be considered. This is
accomplished by tracing a line from the top of each neighboring tree
to the light source. When a particle is being rendered it is checked
to see if it is above or below this line. Points above this line are
not shadowed, and points below this line have a chance of being in
shadow that increases in proportion to the distance from the line.
For the same reasons that shadows could not be perfectly generated for
particles within the trees, the shadows that the trees cast on the
ground must also be approximated. The way this was done was by
rendering an image of the trees from a viewpoint on the ground. This
image was then texture mapped to the ground as a "shadow map." Points
in the image that correspond to trees were rendered as though they
were in shadow.
The actual rendering algorithm used to draw the trees was a modified
painter's algorithm. The first assumption used by this algorithm is
that the bounding volumes of no two trees intersect, so each tree
could be rendered independently. This cuts down on the number of
particles that have to be loaded simultaneously. In addition, instead
of simply depth sorting the particles, they are placed in a number of
depth sorted bins. Inside each bin the particles are simply rendered
in order. This saves time because an exhaustive sort of all particles
does not have to be made. Errors caused by rendering particles in
order inside the bin are masked by the large number of particles.
Using Particle Systems to Model Flocking Birds
The third example of using particle systems was used by Reynolds to
model the behavior of birds moving in a flock [REY87]. In this
particle system the particles are used to represent "boids" (short for
bird-object). This use of a particle system has a few differences
from what was used by Reeves:
Each boid is an
entire polygonal object rather than a graphical primitive
Each boid has a
local coordinate system.
There are a fixed
number of boids - they are not created or destroyed.
Traditional
rendering methods can be used because there are a small number of
boids.
Boids behavior is
dependent on external as well as internal state. In other words, a
boid reacts to what other boids are doing around it.
Boid Behavior Model
Reynolds used observation of real flocks and research of flock
behavior to come up with three primary needs of a boid.
Collision
avoidance - The boid does not wish to collide with other boids or
obstacles.
Velocity
matching - Each boid attempts to go the same speed and direction
as neighboring boids.
Flock
centering - Each boid attempts to stay close to nearby
flockmates.
The boid's movement is made by combining the impulses that are
generated from these three needs. If each need produces a vector that
represents the direction and speed it thinks the boid should move in,
it may not be adequate to simply average these vectors. In the worst
case, these three vectors may be pointing in completely divergent
directions, and the net movement would be zero.
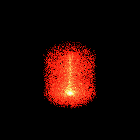
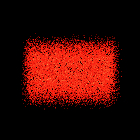
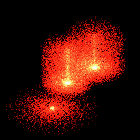
Examples
Here are a few particle system examples that I put together to
demonstrate the process. These examples demonstrate the algorithm
presented by Reeves in [REE83]. Each of the particles maps to a
single pixel in the output image. The particles are translucent, with
the color of multiple particles that map to the same pixel being
additive. In each example the particles are given an initial upwards
trajectory and are acted upon by gravity to give an overall parabolic
path. Except for the example where there are multiple generation
points each of these sequences was created using 20,000 particles and
is rendered to a 256x256 MPEG animation. The number of frames in each
animation varies from 20 to 50.
References
- [REE83]
- W. T. Reeves, "Particle Systems - A Technique for Modeling a Class
of Fuzzy Objects", Computer Graphics, vol. 17, no. 3, pp
359-376, 1983.
- [REE85]
- W. T. Reeves, "Approximate and Probabilistic Algorithms for
Shading and Rendering Structured Particle Systems", Computer
Graphics, vol. 19, no. 3, pp 313-322, 1985.
- [REY87]
- C. W. Reynolds, "Flocks, Herds, and Schools: A Distributed
Behavioral Model", Computer Graphics, vol. 21, no. 4, pp 25-34,
1987.
![[Return to CS563 '95 talks list]](/images/back.gif)
Allen Martin /
amartin@cs.wpi.edu
